(北师大版)2023-2024学年八年级数学上册2.6 实数 同步测试
试卷更新日期:2023-06-28 类型:同步测试
一、选择题
-
1. 在如图所示的数轴上,两点对应的实数分别是和 , 点C到点A的距离与点B到点A的距离相等,则点C所对应的实数是
 ( )
( ) 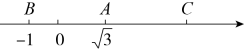 A、 B、 C、 D、2. 若x是非负整数,则表示的值的对应点落在如图数轴上的范围是( )
A、 B、 C、 D、2. 若x是非负整数,则表示的值的对应点落在如图数轴上的范围是( )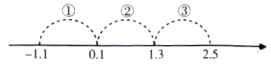 A、① B、② C、③ D、①或②3. 如图,数轴上 , , , 四点中,与对应的点距离最近的是( )
A、① B、② C、③ D、①或②3. 如图,数轴上 , , , 四点中,与对应的点距离最近的是( ) A、点 B、点 C、点 D、点4. 如图,在数轴上,点A,B表示的数分别为-2,2,于点B,且.连接 , 在上截取 , 以点A为圆心,的长为半径画弧,交线段于点E,则点E表示的实数是( )
A、点 B、点 C、点 D、点4. 如图,在数轴上,点A,B表示的数分别为-2,2,于点B,且.连接 , 在上截取 , 以点A为圆心,的长为半径画弧,交线段于点E,则点E表示的实数是( ) A、 B、 C、 D、5. 公元前500年,毕达哥拉斯学派中的一名成员西伯索斯发现了无理数,导致了第一次数学危机.事实上,我国古代发现并阐述无理数的概念比西方更早,但是没有系统的理论.《九章算术》的开方术中指出了存在有开不尽的情形:“若开方不尽者,为不可开.”《九章算术》的作者们给这种“不尽根数”起了一个专门名词—“面”“面”就是无理数.无理数中最具有代表性的数就是“”.下列关于的说法错误的是( )A、可以在数轴上找到唯一一点与之对应 B、它是面积为2的正方形的边长 C、可以用两个整数的比表示 D、可以用反证法证明它不是有理数6. 实数在数轴上的位置如图所示,请化简:=( )
A、 B、 C、 D、5. 公元前500年,毕达哥拉斯学派中的一名成员西伯索斯发现了无理数,导致了第一次数学危机.事实上,我国古代发现并阐述无理数的概念比西方更早,但是没有系统的理论.《九章算术》的开方术中指出了存在有开不尽的情形:“若开方不尽者,为不可开.”《九章算术》的作者们给这种“不尽根数”起了一个专门名词—“面”“面”就是无理数.无理数中最具有代表性的数就是“”.下列关于的说法错误的是( )A、可以在数轴上找到唯一一点与之对应 B、它是面积为2的正方形的边长 C、可以用两个整数的比表示 D、可以用反证法证明它不是有理数6. 实数在数轴上的位置如图所示,请化简:=( ) A、 B、 C、 D、7. 如图所示,在数轴上点A所表示的数为a,CD=1,则a的值为( )
A、 B、 C、 D、7. 如图所示,在数轴上点A所表示的数为a,CD=1,则a的值为( )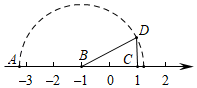 A、 B、-1 C、1 D、-18. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( )
A、 B、-1 C、1 D、-18. 如图,是直角三角形,点C在数轴上对应的数为 , 目 , , 若以点C为圆心,为半径画弧交数轴于点M,则A,M两点间的距离为( ) A、0.4 B、 C、 D、9. 如图,作一个正方形,使其边长为单位长度,以表示数1的点为圆心,正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( )
A、0.4 B、 C、 D、9. 如图,作一个正方形,使其边长为单位长度,以表示数1的点为圆心,正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( )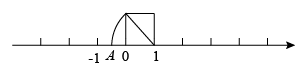 A、 B、 C、 D、10. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
A、 B、 C、 D、10. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )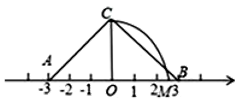 A、 B、4 C、 D、2.5
A、 B、4 C、 D、2.5二、填空题
-
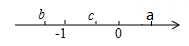
11. 计算:-22+(7-π)0+(-)-1=.12. 已知实数a、b、c在数轴上的位置如图所示,化简代数式|a|-+-的结果等于.
 13. .14. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .15. 计算: .
13. .14. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .15. 计算: .三、解答题
-
16. 实数a、b、c在数轴上的对应点位置如图所示,化简:-|b-c|
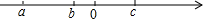 17. 甲同学用如图所示的方法作出C点表示数 , 在中, , , , 且点O,A,C在同一数轴上, .
17. 甲同学用如图所示的方法作出C点表示数 , 在中, , , , 且点O,A,C在同一数轴上, .仿照甲同学的做法,在如图所示的数轴上描出表示的点F.

 18. 阅读理解
18. 阅读理解∵在 , 即 , ∴.∴的整数部分为1,小数
部分为.
解决问题:
已知a是的整数部分,b是的小数部分,求的平方根.
19. 阅读材料:图中是嘉淇同学的作业,老师看了后,问道:“嘉淇同学,你标在数轴上的两个点对应题中的两个无理数,是吗?”嘉淇点点头老师又说:“你这两个无理数对应的点找的非常准确,遗憾的是没有完成全部解答.”
请你帮嘉淇同学完成本次作业.
请把实数0, ,-2, ,1表示在数轴上,并比较它们的大小(用 号连接).
解:

四、综合题
-
20.(1)、计算:;(2)、先化简,再求值: , 其中.21. 阅读与应用:
下面是小敏学习实数之后,写的数学日记的一部分,请你认真阅读,并完成相应的任务.
2022年9月22日 天气:晴
无理数与线段长.今天我们借助勾股定理,在数轴上找到了一些特殊的无理数对应的点,认识了“数轴上的点与实数一一对应”这一事实.
回顾梳理:要在数轴上找到表示的点,关键是在数轴上构造线段 . 如图1,正方形的边长为1个单位长度,以原点O为圆心,对角线长为半径画弧与数轴分别交于点A, , 则点A对应的数为 , 点对应的数为 . 类似地,我们可以在数轴上找到表示 , , …的点.
拓展思考:如图2,改变图1中正方形的位置,用类似的方法作图,可在数轴上构造出线段与 , 其中O仍为原点,点B,分别在原点的右侧、左侧,可由线段与的长得到点B,所表示的无理数!
按照这样的思路,只要构造出特定长度的线段,就能在数轴上找到无理数对应的点!

任务:
(1)、“拓展思考”中,线段的长为 , 的长为;点B表示的数为 , 点表示的数为 .(2)、请从A,B两题中任选一题作答.我选择题.A.请在图3所示的数轴上,画图确定表示的点M,N;
B.请在图3所示的数轴上,画图确定表示的点M.
 22. 实数和数轴上的点一一对应,无理数也可以在数轴上表示出来.
22. 实数和数轴上的点一一对应,无理数也可以在数轴上表示出来. (1)、如图,点O是原点,点A在数轴上,且点A对应的实数为-2,过点A作AB垂直于数轴,且AB=1,连接OB,以O为圆心,OB长为半径画弧,交数轴于点C,那么点C对应的实数为;(2)、在(1)的条件下,若将线段OC向右平移,使得O点对应的实数为1,那么此时C点对应的实数为;(3)、如图,射线AB垂直数轴于点A,点A对应的数是3,请按照(1)中的方法,在数轴上用尺规作出表示的点C(不写作法,保留作图痕迹).23. 如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示 , 设点B所表示的数为m.
(1)、如图,点O是原点,点A在数轴上,且点A对应的实数为-2,过点A作AB垂直于数轴,且AB=1,连接OB,以O为圆心,OB长为半径画弧,交数轴于点C,那么点C对应的实数为;(2)、在(1)的条件下,若将线段OC向右平移,使得O点对应的实数为1,那么此时C点对应的实数为;(3)、如图,射线AB垂直数轴于点A,点A对应的数是3,请按照(1)中的方法,在数轴上用尺规作出表示的点C(不写作法,保留作图痕迹).23. 如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示 , 设点B所表示的数为m.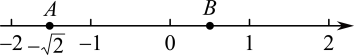 (1)、求的值;(2)、在数轴上还有C、D两点分别表示实数c和d,且有|2c+6|与互为相反数,求2c+3d 的平方根.
(1)、求的值;(2)、在数轴上还有C、D两点分别表示实数c和d,且有|2c+6|与互为相反数,求2c+3d 的平方根.