(北师大版)2023-2024学年八年级数学上册1.3 勾股定理的应用 同步测试
试卷更新日期:2023-06-28 类型:同步测试
一、选择题
-
1. 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
 A、51 B、49 C、76 D、无法确定2. 勾股定理是我国的伟大数学发明之一.如图,以的各边为边向外作正方形,再把较小的两张正方形纸片放入最大的正方形中,三个阴影部分的面积分别为 , , , 则较小两个正方形重叠部分(四边形)的面积为( )
A、51 B、49 C、76 D、无法确定2. 勾股定理是我国的伟大数学发明之一.如图,以的各边为边向外作正方形,再把较小的两张正方形纸片放入最大的正方形中,三个阴影部分的面积分别为 , , , 则较小两个正方形重叠部分(四边形)的面积为( )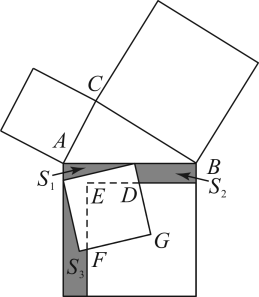 A、4 B、5 C、5.5 D、63. 如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S4=( )
A、4 B、5 C、5.5 D、63. 如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S4=( ) A、2 B、3 C、4 D、64. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( )
A、2 B、3 C、4 D、64. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( ) A、 B、 C、 D、5. 如图,长为的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升至D点,则橡皮筋被拉长了( )
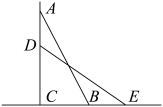
A、 B、 C、 D、5. 如图,长为的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升至D点,则橡皮筋被拉长了( ) A、 B、 C、 D、6. 如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A、 B、 C、 D、6. 如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( ) A、9 B、35 C、45 D、无法计算7. 如图,在“庆国庆,手拉手”活动中,某小组从营地A出发,沿北偏东方向走了1200m到达B点,然后再沿北偏西方向走了500m到达目的地C点,此时A,C两点之间的距离为( )
A、9 B、35 C、45 D、无法计算7. 如图,在“庆国庆,手拉手”活动中,某小组从营地A出发,沿北偏东方向走了1200m到达B点,然后再沿北偏西方向走了500m到达目的地C点,此时A,C两点之间的距离为( ) A、1000m B、1100m C、1200m D、1300m8. 如图,一棵大树在一次强台风中于离地面10m处折断倒下,倒下部分的树梢到树的距离为24m,则这棵大树折断处到树顶的长度是( )
A、1000m B、1100m C、1200m D、1300m8. 如图,一棵大树在一次强台风中于离地面10m处折断倒下,倒下部分的树梢到树的距离为24m,则这棵大树折断处到树顶的长度是( ) A、10m B、15m C、26m D、30m9. 如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米.若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A、10m B、15m C、26m D、30m9. 如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米.若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( ) A、1米 B、米 C、2米 D、4米10. 如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门铃5m及5m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD的长为( )
A、1米 B、米 C、2米 D、4米10. 如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门铃5m及5m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD的长为( ) A、3米 B、4米 C、5米 D、7米
A、3米 B、4米 C、5米 D、7米二、填空题
-
11. 如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,米,则BE=米.
 12. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.
12. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.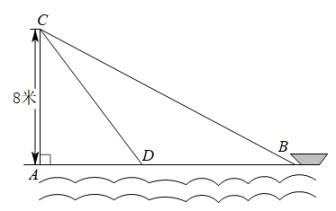 13. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米.
13. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米. 14. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .
14. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .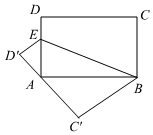 15. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:“有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的处,水深和芦苇长各是多少尺?”则该问题的水深是 .
15. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:“有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的处,水深和芦苇长各是多少尺?”则该问题的水深是 .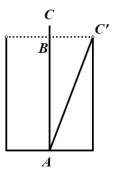
三、解答题
-
16. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m)
 17. 某地一楼房发生火灾,消防队员决定用消防车上的云梯救人如图(1).如图(2),已知云梯最多只能伸长到(即),消防车高 , 救人时云梯伸长至最长,在完成从(即)高的处救人后,还要从(即)高的处救人,这时消防车从处向着火的楼房靠近的距离为多少米?(延长交于点 , , 点在上,的长即为消防车的高)
17. 某地一楼房发生火灾,消防队员决定用消防车上的云梯救人如图(1).如图(2),已知云梯最多只能伸长到(即),消防车高 , 救人时云梯伸长至最长,在完成从(即)高的处救人后,还要从(即)高的处救人,这时消防车从处向着火的楼房靠近的距离为多少米?(延长交于点 , , 点在上,的长即为消防车的高)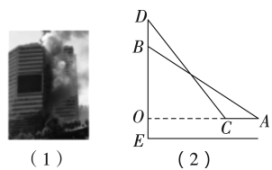 18. 如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB.
18. 如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB. 19. 如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B′离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
19. 如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B′离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.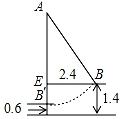
四、综合题
-
20. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB .
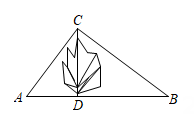
(1)、求修建的公路CD的长;(2)、若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?21. 如图,某火车站内部墙面上有破损处(看作点A),现维修师傅需借助梯子完成维修工作.梯子的长度为 , 将其斜靠在这面墙上,测得梯子底部E离墙角N处 , 维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D距离墙面破损处 . (1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?22. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)、该火车站墙面破损处A距离地面有多高?(2)、如果维修师傅要使梯子顶部到地面的距离为4.8m.那么梯子底部需要向墙角方向移动多少米?22. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.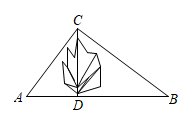 (1)、求修建的公路CD的长;(2)、若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?23. 在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某种原由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得千米,千米,千米.
(1)、求修建的公路CD的长;(2)、若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?23. 在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某种原由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得千米,千米,千米.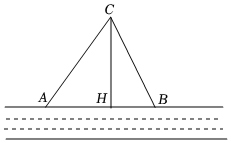 (1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明.(2)、求原来的路线AC的长.
(1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明.(2)、求原来的路线AC的长.