福建省2023年中考数学试卷
试卷更新日期:2023-06-28 类型:中考真卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
-
1. 下列实数中,最大的数是( )A、 B、0 C、1 D、22. 下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 若某三角形的三边长分别为3,4,m,则m的值可以是( )A、1 B、5 C、7 D、94. 党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,教育普及水平实现历史性跨越,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五.将数据1040000000用科学记数法表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 根据福建省统计局数据,福建省2020年的地区生产总值为43903.89亿元,2022年的地区生产总值为53109.85亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )A、 B、 C、 D、7. 阅读以下作图步骤:
3. 若某三角形的三边长分别为3,4,m,则m的值可以是( )A、1 B、5 C、7 D、94. 党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,教育普及水平实现历史性跨越,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五.将数据1040000000用科学记数法表示为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 根据福建省统计局数据,福建省2020年的地区生产总值为43903.89亿元,2022年的地区生产总值为53109.85亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )A、 B、 C、 D、7. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且8. 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求,学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.
A、且 B、且 C、且 D、且8. 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求,学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.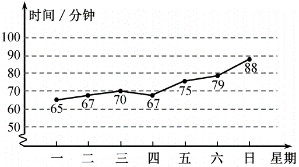
根据统计图,下列关于小亮该周每天校外锻炼时间的描述,正确的是( )
A、平均数为70分钟 B、众数为67分钟 C、中位数为67分钟 D、方差为09. 如图,正方形四个顶点分别位于两个反比例函数和的图象的四个分支上,则实数的值为( )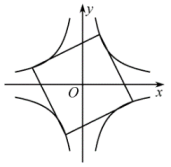 A、 B、 C、 D、310. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )
A、 B、 C、 D、310. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )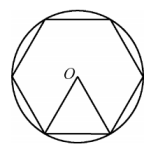 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题:本题共6小题,每小题4分,共24分.
-
11. 某仓库记账员为方便记账,将进货10件记作 , 那么出货5件应记作 .12. 如图,在中,为的中点,过点且分别交于点 . 若 , 则的长为 .
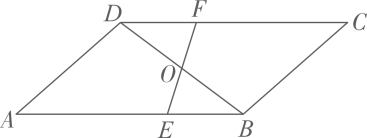 13. 如图,在菱形中, , 则的长为 .
13. 如图,在菱形中, , 则的长为 .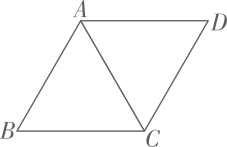 14. 某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:
14. 某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:项目
应聘者
综合知识
工作经验
语言表达
甲
75
80
80
乙
85
80
70
丙
70
78
70
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是 .
15. 已知 , 且 , 则的值为 .16. 已知抛物线经过两点,若分别位于抛物线对称轴的两侧,且 , 则的取值范围是 .三、解答题:本题共9小题,共86分。解答应写出文字说明、证明过程或演算步骤。
-
17. 计算: .18. 解不等式组:19. 如图, .
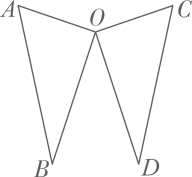
求证: .
20. 先化简,再求值: , 其中 .21. 如图,已知内接于的延长线交于点 , 交于点 , 交的切线于点 , 且 . (1)、求证:;(2)、求证:平分 .22. 为促进消费,助力经济发展,某商场决定“让利酬宾”,于“五一”期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小质地完全相同的1个红球及编号为①②③的3个黄球的袋中,随机摸出1个球,若摸得红球,则中奖,可获得奖品:若摸得黄球,则不中奖.同时,还允许未中奖的顾客将其摸得的球放回袋中,并再往袋中加入1个红球或黄球(它们的大小质地与袋中的4个球完全相同),然后从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,若摸得的两球的颜色相同,则该顾客可获得精美礼品一份.现已知某顾客获得抽奖机会.(1)、求该顾客首次摸球中奖的概率;(2)、假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由23. 阅读下列材料,回答问题
(1)、求证:;(2)、求证:平分 .22. 为促进消费,助力经济发展,某商场决定“让利酬宾”,于“五一”期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小质地完全相同的1个红球及编号为①②③的3个黄球的袋中,随机摸出1个球,若摸得红球,则中奖,可获得奖品:若摸得黄球,则不中奖.同时,还允许未中奖的顾客将其摸得的球放回袋中,并再往袋中加入1个红球或黄球(它们的大小质地与袋中的4个球完全相同),然后从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,若摸得的两球的颜色相同,则该顾客可获得精美礼品一份.现已知某顾客获得抽奖机会.(1)、求该顾客首次摸球中奖的概率;(2)、假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由23. 阅读下列材料,回答问题任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大度远大于南北走向的最大宽度,如图1.
工具:一把皮尺(测量长度略小于)和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度);测角仪的功能是测量角的大小,即在任一点处,对其视线可及的两点,可测得的大小,如图3.

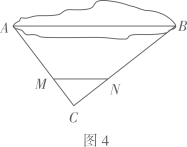
小明利用皮尺测量,求出了小水池的最大宽度 , 其测量及求解过程如下:测量过程:
(ⅰ)在小水池外选点 , 如图4,测得;
(ⅱ)分别在上测得;测得 . 求解过程:
由测量知, ,
, 又①____,
.
又②____( .
故小水池的最大宽度为____ .
(1)、补全小明求解过程中①②所缺的内容;(2)、小明求得用到的几何知识是;(3)、小明仅利用皮尺,通过5次测量,求得 . 请你同时利用皮尺和测角仪,通过测量长度、角度等几何量,并利用解直角三角形的知识求小水池的最大宽度 , 写出你的测量及求解过程.要求:测量得到的长度用字母表示,角度用表示;测量次数不超过4次(测量的几何量能求出 , 且测量的次数最少,才能得满分).