广西壮族自治区2023年中考数学试卷
试卷更新日期:2023-06-28 类型:中考真卷
一、单项选择题(本大题共12小题,每小题3分.)
-
1. 若零下2摄氏度记为 , 则零上2摄氏度记为( )A、 B、 C、 D、2. 下列数学经典图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若分式有意义,则x的取值范围是( )A、 B、 C、 D、4. 如图,点A、B、C在上, , 则的度数是( )
3. 若分式有意义,则x的取值范围是( )A、 B、 C、 D、4. 如图,点A、B、C在上, , 则的度数是( ) A、 B、 C、 D、5. 在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 在数轴上表示正确的是( )A、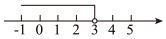 B、
B、 C、
C、 D、
D、 6. 甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下: , , , , 则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 如图,一条公路两次转弯后又回到与原来相同的方向,如果 , 那么的度数是( )
6. 甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下: , , , , 则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁7. 如图,一条公路两次转弯后又回到与原来相同的方向,如果 , 那么的度数是( ) A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 将抛物线 向右平移3个单位,再向上平移4个单位,得到的抛物线是( )A、 B、 C、 D、10. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 将抛物线 向右平移3个单位,再向上平移4个单位,得到的抛物线是( )A、 B、 C、 D、10. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
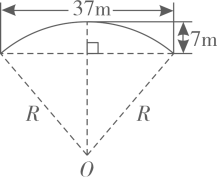 A、 B、 C、 D、11. 据国家统计局发布的《2022年国民经济和社会发展统计公报》显示,2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元.设2020年至2022年全国居民人均可支配收入的年平均增长率为x,依题意可列方程为( )A、 B、 C、 D、12. 如图,过的图象上点A,分别作x轴,y轴的平行线交的图象于B,D两点,以 , 为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为 , , , , 若 , 则的值为( )
A、 B、 C、 D、11. 据国家统计局发布的《2022年国民经济和社会发展统计公报》显示,2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元.设2020年至2022年全国居民人均可支配收入的年平均增长率为x,依题意可列方程为( )A、 B、 C、 D、12. 如图,过的图象上点A,分别作x轴,y轴的平行线交的图象于B,D两点,以 , 为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为 , , , , 若 , 则的值为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 化简: = .14. 分解因式:a2 + 5a =.15. 函数的图象经过点 , 则 .16. 某班开展“梦想未来、青春有我”主题班会,第一小组有2位男同学和3位女同学,现从中随机抽取1位同学分享个人感悟,则抽到男同学的概率是 .17. 如图,焊接一个钢架,包括底角为的等腰三角形外框和3m高的支柱,则共需钢材约m(结果取整数).(参考数据: , , )
 18. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
18. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .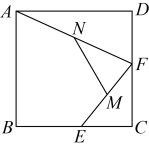
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算: .20. 解分式方程: .21. 如图,在中, , .
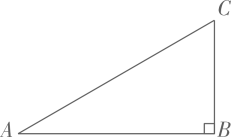 (1)、在斜边上求作线段 , 使 , 连接;
(1)、在斜边上求作线段 , 使 , 连接;(要求:尺规作图并保留作图痕迹,不写作法,标明字母)
(2)、若 , 求的长.22. 4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,航阳中学开展了“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取20名学生的成绩进行统计分析(6分及6分以上为合格),数据整理如下:学生成绩统计表
七年级
八年级
平均数
7.55
7.55
中位数
8
c
众数
a
7
合格率
b
85%

根据以上信息,解答下列问题:
(1)、写出统计表中a,b,c的值;(2)、若该校八年级有600名学生,请估计该校八年级学生成绩合格的人数;(3)、从中位数和众数中任选其一,说明其在本题中的实际意义.23. 如图,平分 , 与相切于点A,延长交于点C,过点O作 , 垂足为B. (1)、求证:是的切线;(2)、若的半径为4, , 求的长.24. 如图,是边长为4的等边三角形,点D,E,F分别在边 , , 上运动,满足 .
(1)、求证:是的切线;(2)、若的半径为4, , 求的长.24. 如图,是边长为4的等边三角形,点D,E,F分别在边 , , 上运动,满足 . (1)、求证:;(2)、设的长为x,的面积为y,求y关于x的函数解析式;(3)、结合(2)所得的函数,描述的面积随的增大如何变化.25. 【综合与实践】
(1)、求证:;(2)、设的长为x,的面积为y,求y关于x的函数解析式;(3)、结合(2)所得的函数,描述的面积随的增大如何变化.25. 【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤.小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得:.其中秤盘质量克,重物质量m克,秤砣质量M克,秤纽与秤盘的水平距离为l厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.

【方案设计】
目标:设计简易杆秤.设定 , , 最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
任务一:确定l和a的值.
(1)、当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;(2)、当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于l,a的方程;(3)、根据(1)和(2)所列方程,求出l和a的值.任务二:确定刻线的位置.
(4)、根据任务一,求y关于m的函数解析式;(5)、从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离.26. 【探究与证明】折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.
【动手操作】如图1,将矩形纸片对折,使与重合,展平纸片,得到折痕;折叠纸片,使点B落在上,并使折痕经过点A,得到折痕 , 点B,E的对应点分别为 , , 展平纸片,连接 , , .

请完成:
(1)、观察图1中 , 和 , 试猜想这三个角的大小关系;(2)、证明(1)中的猜想;【类比操作】如图2,N为矩形纸片的边上的一点,连接 , 在上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕;折叠纸片,使点B,P分别落在 , 上,得到折痕l,点B,P的对应点分别为 , , 展平纸片,连接, .
 (3)、证明是的一条三等分线.
(3)、证明是的一条三等分线.