河南省南阳市桐柏县2022-2023学年八年级下册6月月考数学试卷

试卷更新日期：2023-06-28 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 据相关资料显示，目前发现的一种新型病毒的直径约为120nm（1nm＝10^-9m），120nm用科学记数法表示是（）

A、120×10^-9m B、1.20×10^-9m C、1.20×10^-7m D、0.12×10^-6m

查看试题解析
2. 如图，点E在▱ABCD的对角线AC上，AE＝BE＝AD，∠D＝105°，则∠ACB的度数是（）

A、45° B、50° C、55° D、60°

查看试题解析
3. 如图，四边形ABCD的对角线AC，BD相交于点O，且AC⊥BD，则下列条件能判定四边形ABCD是菱形的是（）

A、 $A B = C D$ B、 $A B ∥ C D$ ， $A B = C D$ C、 $A C = B D$ D、 $∠ A B C = ∠ D C B$

查看试题解析
4. 如图，在中国象棋的棋盘上，建立适当的平面直角坐标系，使“帅”的坐标是（2，0），“兵”的坐标为（1，4），那么“车”的坐标是（）

A、（-2，2） B、（-2，1） C、（-1，1） D、（-2，0）

查看试题解析
5. 如图，E是边长为6的正方形ABCD对角线上的一动点，若四边形EFCG为矩形，则矩形EFCG的周长为（）

A、6 B、10 C、12 D、无法确定

查看试题解析
6. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ ）的图象上有一点P，PA⊥x轴于点A，点B在y轴上，△PAB的面积为6，则k的值为（）

A、-12 B、12 C、6 D、-6

查看试题解析
7. 物美超市试销一批新款衬衫，一周内销售情况如下表所示，超市经理想要了解哪种型号最畅销，那么他最关注的统计量应该是（）
型号（厘米）
38
39
40
41
42
43
数量（件）
13
21
35
48
26
8

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
8. 已知关于x的分式方程 $\frac{3 x + n}{2 x + 1} = 2$ 的解是负数，则n的取值范围为（）

A、n＞1且 $n \neq \frac{1}{2}$ B、n＞1 C、n＜2且 $n \neq \frac{3}{2}$ D、n＜2

查看试题解析
9. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若AE＝8，AB＝5，则BF的长为（）

A、5 B、6 C、8 D、12

查看试题解析
10. 如图1，在矩形ABCD中，动点P从点B出发，沿B→C→D→A方向匀速运动至点A停止．已知点P的运动速度为1cm/s，设点P的运动时间为x（s），△PAB的面积为y（cm²），若y关于x的函数图象如图2所示，则矩形对角线AC的长为（）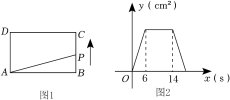

A、5 B、6 C、8 D、10

查看试题解析

二、填空题（每小题3分，共15分）

11. 计算： ${(- \frac{1}{2})}^{- 3} - {(- π)}^{0} =$ .

查看试题解析
12. 关于x的方程 $\frac{m}{x - 2} - \frac{1}{2 - x} = 1$ 有增根，则m的值为．

查看试题解析
13. 有6个数据的平均数为25，另有9个数据的平均数是20，那么所有这15个数据的平均数是．

查看试题解析
14. 已知点P（3，y₁），Q（-2，y₂）在一次函数y＝（-4m+1）x+2的图象上，若y₁＜y₂ ，则实数m的取值范围是．

查看试题解析
15. 如图，在四边形ABCD中，AB∥CD，BC⊥CD，AB＝8cm，DC＝10cm，E是DC上一点，且DE＝3，P从A点出发以1cm/s的速度向B点运动，同时Q从D点出发以2cm/s的速度向C点运动，当其中一点到达终点时，另一点也随之停止，设运动时间为t（s），当t＝时，以A、P、E、Q为顶点的四边形是平行四边形．

查看试题解析

三、解答题（共8小题）

16.

(1)、解分式方程： $\frac{2 - x}{x - 3} + 3 = \frac{1}{3 - x}$ ；

(2)、先化简 $(\frac{m^{2} + 2 m}{m^{2} + 4 m + 4} + 1) \div \frac{m^{2} - 1}{m^{2} - m}$ ，再从-2，-1，0，1，2中选取一个合适的数作为m的值代入求值．

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A E ⊥ B D$ ， $C F ⊥ B D$ ，垂足分别为点 $E$ ， $F$ .

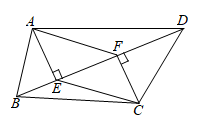(1)、请你只添加一个条件（不另加辅助线），使得四边形 $A E C F$ 为平行四边形，你添加的条件是；

(2)、添加了条件后，证明四边形 $A E C F$ 为平行四边形.

查看试题解析

18. 某水果批发商以5元/kg的成本价新进500箱库尔勒香梨，每箱质量10kg，在出售香梨前，需要去掉损坏的香梨，现随机抽取20箱，去掉损坏香梨后称得每箱的质量（单位：kg）如下：

9.7	9.8	9.6	9.5	9.8	9.9	9.8	9.7	9.8	9.7
9.8	9.9	9.7	9.8	9.5	9.7	9.7	9.9	9.7	10.0

整理数据：

质量（kg）	9.5	9.6	9.7	9.8	9.9	10.0
数量（箱）	2	1	7	a	3	1

分析数据：

平均数	众数	中位数
9.75	b	c

(1)、直接写出上述表格中a＝， b＝， c＝．

(2)、按样本平均数估算这500箱香梨共损坏了多少千克？

(3)、根据（2）中的结果，问该水果批发商销售这批香梨每千克售价至少定为多少元才不亏本？（结果保留一位小数）

查看试题解析

19. 如图，四边形ABCD的对角线AC，BD相交于点O，四边形OBEC是矩形，△BOC≌△DOA．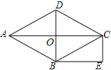

(1)、求证：四边形ABCD是菱形．

(2)、若BC＝13，AC＝24，求菱形ABCD的面积．

查看试题解析
20. 如图，一次函数y₁＝k₁x+b的图象与反比例函数 $y_{2} ＝ \frac{k_{2}}{x} （ x ＜ 0 ）$ 的图象交于第二象限内的点A（-4，2）和B（-2，m），与x轴交于点C．

(1)、分别求出这两个函数的表达式．

(2)、不等式 $k_{1} x + b \leq \frac{k_{2}}{x}$ 的解集是．

(3)、在坐标平面内是否存在点P，使得由点O，B，C，P组成的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
21. 如图，在矩形ABCD中，点M是边AD的中点，点P是边BC上的动点，PE⊥MC，PF⊥BM，垂足为点E，F．

(1)、当矩形ABCD的长与宽满足什么条件时，四边形PEMF为矩形？证明你的结论；

(2)、如果四边形PEMF为矩形，那么当点P运动到什么位置时，矩形PEMF变为正方形？能证明你的猜想吗？

查看试题解析
22. 今年的冬奥会点燃了青少年的“冰雪热”，推动了冰雪产业经济．某体育运动器材商店的滑雪护目镜和滑雪头盔成了热销商品．已知滑雪头盔比滑雪护目镜的进价高50元，商店用4000元购进的滑雪头盔与用3000元购进的滑雪护目镜数量一样多．

(1)、求滑雪护目镜和滑雪头盔的进价；

(2)、该商店计划购进滑雪护目镜和滑雪头盔共200个，且滑雪护目镜的数量不少于滑雪头盔的2倍．购进后，滑雪护目镜按高于进价18%定价，滑雪头盔按高于进价15%定价．假设该商店购进的这两种商品最后均能按定价售出，请你求出该商店能获得最大利润的进货方案．

查看试题解析
23. 如图1，在Rt△EAF中，∠A＝90°，∠AEF，∠AFE的外角平分线交于点C，过点C分别作直线AB，AD的垂线，B，D为垂足．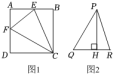

(1)、【问题发现】
∠ECF＝°（直接写出结果，不写解答过程）．

(2)、【问题探究】
①求证：四边形ABCD是正方形．
②若AF＝DF＝4，求BE的长．

(3)、【问题拓展】
如图2，在△PQR中，∠QPR＝45°，高PH＝4，HR＝1，则HQ的长度是（直接写出结果，不写解答过程）．

查看试题解析

型号（厘米）	38	39	40	41	42	43
数量（件）	13	21	35	48	26	8