(北师大版)2023-2024学年九年级数学上册1.1 菱形的性质与判定 同步测试
试卷更新日期:2023-06-28 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,AD⊥BC于D,E,F分别是AB,AC的中点,连接DE,DF,当△ABC满足下列哪个条件时,四边形AEDF为菱形( )
 A、AB=AC B、∠B=∠A C、BD=DF D、DE⊥DF2. 如图,某同学剪了两条宽均为的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( ).
A、AB=AC B、∠B=∠A C、BD=DF D、DE⊥DF2. 如图,某同学剪了两条宽均为的纸条,交叉叠放在一起,且它们的交角为60°,则它们重叠部分的面积为( ). A、3 B、 C、 D、63. 如图,在▱ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
A、3 B、 C、 D、63. 如图,在▱ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( ) A、OE=OF B、AE=CF C、EF⊥AC D、EF=AC4. 如图,菱形ABCD中,∠BAD=60°,AC、BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG、AE.则下列结论:①OG=AB; ②四边形ABDE是菱形;③S四边形ODGF=S△ABF;其中正确的是( )
A、OE=OF B、AE=CF C、EF⊥AC D、EF=AC4. 如图,菱形ABCD中,∠BAD=60°,AC、BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG、AE.则下列结论:①OG=AB; ②四边形ABDE是菱形;③S四边形ODGF=S△ABF;其中正确的是( ) A、①② B、①③ C、②③ D、①②③5. 已知菱形的面积为 , 一条对角线长为 , 则它的边长为( )A、 B、 C、 D、6. 菱形ABCD的两条对角线AC=8cm,BD=6cm,那么菱形的边长是( )A、6cm B、5cm C、4cm D、8cm7. 如图,点E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,四边形ABCD应具备的条件是( )
A、①② B、①③ C、②③ D、①②③5. 已知菱形的面积为 , 一条对角线长为 , 则它的边长为( )A、 B、 C、 D、6. 菱形ABCD的两条对角线AC=8cm,BD=6cm,那么菱形的边长是( )A、6cm B、5cm C、4cm D、8cm7. 如图,点E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,四边形ABCD应具备的条件是( ) A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分8. 菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角相等 D、对边平行9. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°, , , 若AD=2,则四边形CODE的周长为( )
A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分8. 菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角相等 D、对边平行9. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°, , , 若AD=2,则四边形CODE的周长为( ) A、12 B、10 C、8 D、410. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )
A、12 B、10 C、8 D、410. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )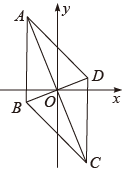 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在周长为16的菱形中,点E、F分别在边上, , P为上一动点,则线段长度的最小值为.
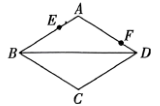 12. 如图,菱形的对角线 , 相交于点 , 按下列步骤作图:
12. 如图,菱形的对角线 , 相交于点 , 按下列步骤作图:①分别以点 , 为圆心,大于的长为半径画弧,两弧的交点分别为点 , ;
②过点 , 作直线 , 交于点;
③连接.若 , 则菱形的周长为.
 13. 如图,四边形是菱形, , , 于点 , 则 .
13. 如图,四边形是菱形, , , 于点 , 则 . 14. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作于点H,连接OH,若 , , 则菱形ABCD的面积为 .
14. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作于点H,连接OH,若 , , 则菱形ABCD的面积为 . 15. 如图,已知四边形是平行四边形,从① , ② , ③中选择一个作为条件,补充后使四边形成为菱形,则应选择(填序号).
15. 如图,已知四边形是平行四边形,从① , ② , ③中选择一个作为条件,补充后使四边形成为菱形,则应选择(填序号).
三、解答题
-
16. 如图,点E是菱形ABCD的边BC延长线上一点,AC是对角线,∠BAC:∠ACE=2:7,求∠B的度数.
 17. 如图,在菱形中,分别延长、到E、F,使得 , 连接、.求证:.
17. 如图,在菱形中,分别延长、到E、F,使得 , 连接、.求证:.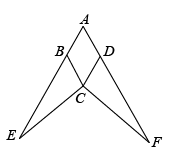 18. 如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE,CF.求证:四边形AECF是菱形.
18. 如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE,CF.求证:四边形AECF是菱形. 19. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: .
19. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: .
四、综合题
-
20. 在菱形中,.(1)、以线段为边求作菱形;(要求:尺规作图,不写作法,保留作图痕迹)
 (2)、若菱形的面积为 , 求的长.21. 如图,在四边形中, , 对角线 , 交于点 , , 且平分 , 过点作交的延长线于点.
(2)、若菱形的面积为 , 求的长.21. 如图,在四边形中, , 对角线 , 交于点 , , 且平分 , 过点作交的延长线于点. (1)、求证:四边形是菱形;(2)、若 , , 求的面积.
(1)、求证:四边形是菱形;(2)、若 , , 求的面积.

