浙江省宁波市海曙区2022-2023学年六年级下学期数学毕业考试试卷
试卷更新日期:2023-06-27 类型:小升初真题
一、选择题(共10分)
-
1. 下面各数中“8”表示的意义不同的是( )。A、0.80 B、 C、8% D、0.08
-
2. 象棋规则口诀中有“马走日”、“象走田”的说法。在下面的棋局中,如果用“象”吃掉对方的“兵”,应该向( )方向走。
 A、西北 B、东北 C、西南 D、东南
A、西北 B、东北 C、西南 D、东南 -
3. 魏晋时期的数学家刘徽从圆内接正六边形开始,将边数逐次加倍,得到的圆内接正多边形就逐步逼近圆,为此来计算圆的周长、面积以及圆周率。这种方法称为( )。A、刘徽法 B、近圆术 C、圆中方 D、割圆术
-
4. 浙江省的占地面积约105500平方千米,宁波市的面积大约是( )平方千米。
 A、50000 B、20000 C、10000 D、5000
A、50000 B、20000 C、10000 D、5000 -
5. 王芳用小正方体积木搭成的图形,从上面看到的图形如下图(积木上的数字表示这个位置上所用的小正方体的个数),从前面看到的图形是( )。
 A、
A、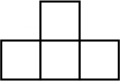 B、
B、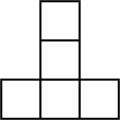 C、
C、 D、
D、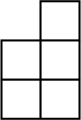
-
6. 仓库里有短袖衬衫1800件,是长袖衬衫数的75%,短袖和长袖衬衫一共多少件?下面解法中,不正确是( )。A、1800÷75%+1800 B、1800∶3=x∶(3+4) C、1800÷3×(3+4) D、1800×(1+)
-
7. 下面是乐乐计算23×12的思路,他用①、②、③、④四个区域来表示计算过程。算式中“←”所指向的“3”表示( )区域的意思。
 A、① B、② C、③ D、④
A、① B、② C、③ D、④ -
8. 在研究梯形的面积公式时,下列面积计算方法的思路和对应的算式错误的是( )。A、
 (a+b)h÷2
B、
(a+b)h÷2
B、 ah÷2+bh÷2
C、
ah÷2+bh÷2
C、 ah÷2+(b-a)h÷2
D、
ah÷2+(b-a)h÷2
D、 (a+b)+bh÷2
(a+b)+bh÷2
-
9. 下列说法正确的是( )。A、从0~9这10张数字卡片中,任意抽取1张,抽到比5大的数字的可能性比较大 B、一个笔盒提价20%后又降价20%,价格不变。 C、表示一周内气温的变化情况,选用折线统计图比较合适。 D、所有的偶数都是合数。
-
10. 如图,在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退。开始时骰子如图(1)那样摆放,朝上的点数是1;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能是下列数中的( )。
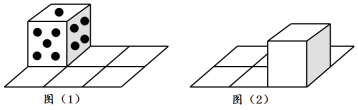 A、2 B、4 C、5 D、6
A、2 B、4 C、5 D、6
二、填空题(共26分)
-
11. 第十九届亚运会将于2023年9月23日在浙江省杭州市举行,作为亚运会主场馆的杭州奥体博览城核心区占地面积为一百五十四万三千七百平方米,横线上的数写作。
-
12. ∶10=4∶5==%=成
-
13.
3.2吨=千克
64000平方米=公顷
5升60毫升=升
2.15时=时分
-
14. 中国结是一种具有中国特色的手工编织工艺品,它代表着团结、吉祥和平安,深受人们的喜爱。用一根5米长的红绳正好可以编织8个中国结,每个中国结用了这根红绳的 , 每个中国结用了米的红绳。
-
15. m=2×2×3,n=2×3×5,m和n的最大公因数是 , 最小公倍数是。
-
16. 如图,如果点A表示的数是1,则点B表示的数是;如果点C表示的数是1,则点A表示的数是。

-
17. 根据 , , 可以得出=÷(填整数)。
-
18. 如图,在平衡架的左侧已挂上了5个相同质量的砝码,在右边第5格处必须挂个相同质量的砝码,才能使平衡架平衡。

-
19. 2023年五一期间,旅游市场爆发式增长,浙江省旅游人数创历史新高。其中杭州市接待游客量为661.8万人次,比宁波的1.5倍少50.25万人次。宁波市接待的游客约有多少万人次?应设约有x万人次,列方程为。
-
20. 把一个半径为10cm的圆形贴纸剪成大小相同的若干片,已经用掉了3片(如下图),剩下贴纸的面积为cm²,周长为cm。

-
21. 张明计划使用木条制作一个长方体框架,已经制作了一部分(如上图),还需要根5厘米长的木条。如果想为这个框架每个角装上防撞角,那么一共需要安装个。

-
22. 如图,张亮在计算机课上编制了一个计算小程序,输入一个数后,小程序通过计算会输出另一个数。请根据发现的规律解决以下问题。
 (1)、输入 , 输出47;(2)、如果输入a,输出。
(1)、输入 , 输出47;(2)、如果输入a,输出。
三、计算题(共24分)
-
23. 直接写出得数
0.57+4.3=
×=
73×101=
-=
2.4÷0.1=
2.6×-×0.6=
-
24. 用合理的方法计算,并写出过程
①4×(250-400÷16)
②5.5÷×
③3.6×+6.4×
④7-7×+
⑤+4.9++5.1
⑥(-0.8+)×12.5
-
25. 解方程
①x∶=12∶
②-2.6=5.4
③-=
四、图形与几何(共12分)
-
26. 图中每个小方格的边长是1cm,请按要求完成下面各题。
 (1)、图中点A的位置用数对(4,5)表示,点B的位置用数对表示,点C的位置用数对 表示。(2)、画出三角形ABC绕点A逆时针旋转90°后的图形。(3)、画出三角形ABC按2∶1放大后的图形。(4)、将三角形ABC绕AC边旋转一周,会得到一个立体图形,列出计算这个立体图形体积的算式:。(不求出结果)
(1)、图中点A的位置用数对(4,5)表示,点B的位置用数对表示,点C的位置用数对 表示。(2)、画出三角形ABC绕点A逆时针旋转90°后的图形。(3)、画出三角形ABC按2∶1放大后的图形。(4)、将三角形ABC绕AC边旋转一周,会得到一个立体图形,列出计算这个立体图形体积的算式:。(不求出结果) -
27. 一张长10cm,宽6cm的长方形纸按下图方式对折,求出最后梯形的面积

五、解决问题(共28分)
-
28. 某工程队铺一段路,原计划每天铺9.6千米,15天铺完,实际每天比原计划多铺2.4千米,实际要用多少天铺完?
-
29. 三年疫情结束,经济逐渐复苏。

2023年第一季度出口额为多少万亿元?
-
30. 在学习了圆柱和圆锥的体积之后,王华做了一个圆柱形容器和一些圆锥形容器,并进行了下面两个试验。(单位:cm)(1)、试验一:王华在圆柱形容器里面装了一些水(如下图),再将这些水倒入下面一个圆锥形容器中,倒入圆锥形容器中能恰好倒满。

 (2)、试验二:王华按照下面的步骤测量了一个土豆的体积。
(2)、试验二:王华按照下面的步骤测量了一个土豆的体积。
根据上面的测量结果,你能求出这个土豆的体积是多少立方厘米吗?
-
31. 在教室里安装空调时需要考虑制冷量。房间需要的制冷量=单位制冷量×房间面积。一般情况下,这个“单位制冷量”的基础为160~180瓦/平方米。(1)、教室长8米,宽7米,安装空调时应该考虑的制冷量最少是多少瓦?(2)、后勤处准备在第(1)题中的教室里安装两台同一型号的空调,请你根据下表作出选择,并说明理由。
型号
1P
1.5P
2P
3P
制冷量/瓦
2200-2600
3200-3600
4500-5100
6500-7300
-
32. 如图所示,四边形ABCD是长方形,点P从A出发沿顺时针方向运动,速度为1厘米/秒。下图是三角形PAB的面积随着时间的变化情况,当运动时间为2秒时,三角形PAB的面积为16平方厘米。
 (1)、AB长cm,AD长cm。(2)、当运动时间为秒时,点P运动到点C的位置。(3)、连接BD。若BD与AP相交于M,当三角形PBM的面积与三角形ABM的面积之比为1:2时,求点P的运动时间(画出草图,再解答)。
(1)、AB长cm,AD长cm。(2)、当运动时间为秒时,点P运动到点C的位置。(3)、连接BD。若BD与AP相交于M,当三角形PBM的面积与三角形ABM的面积之比为1:2时,求点P的运动时间(画出草图,再解答)。
