安徽省皖北县中联盟2022-2023学年高一下册5月联考数学试卷
试卷更新日期:2023-06-26 类型:月考试卷
一、单选题
-
1. 若复数是纯虚数,则实数a的值是( )A、1 B、0 C、 D、2. 下列叙述正确的是( )A、用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台 B、两个面平行且相似,其余各面都是梯形的多面体是棱台 C、有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台 D、棱台的侧棱延长后必交于一点3. 已知向量 , , 若 , 则( )A、 B、 C、0 D、14. 如图所示,是水平放置的的斜二测直观图,其中 , 则是( )
 A、锐角三角形 B、钝角三角形 C、等腰直角三角形 D、以上选项都不对5. 已知平面 、 、 两两垂直,直线 、 、 满足: , , ,则直线 、 、 不可能满足以下哪种关系( )
A、锐角三角形 B、钝角三角形 C、等腰直角三角形 D、以上选项都不对5. 已知平面 、 、 两两垂直,直线 、 、 满足: , , ,则直线 、 、 不可能满足以下哪种关系( )
A、两两垂直 B、两两平行 C、两两相交 D、两两异面6. 已知复数满足 , 则下列结论正确的是( )A、 B、的虚部与实部相等 C、 D、存在复数 , 使7. 位于某港口A的小艇要将一件重要物品送到一艘正在航行的海轮上.在小艇出发时,海轮位于港口A北偏东30°且与该港口相距30海里的B处,并正以20海里/时的速度沿正西方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与海轮相遇.若希望相遇时小艇的航行距离最小,则小艇的航行速度(单位:海里/时)应为( )A、 B、20 C、 D、8. 在边长为6的菱形中, , 现将菱形沿对角线BD折起,当时,三棱锥外接球的表面积为( )A、 B、 C、 D、二、多选题
-
9. 下列说法正确的是( )A、复数的虚部为 B、方程的复数根为 C、若 , 则复平面内对应的点位于第二象限 D、复平面内,实轴上的点对应的复数是实数10. 已知的内角A,B,C所对的边分别为a,b,c,则下列说法正确的是( )A、 B、若为斜三角形,则 C、若 , 则是锐角三角形 D、若 , 则一定是等边三角形11. 如图,正四棱柱中, , E,F分别为 , 的中点,则下列结论错误的是( )
 A、平面BEF B、直线与直线BF所成的角为 C、平面BEF与平面ABCD的夹角为 D、直线与平面ABCD所成的角为12. 已知正的边长为 , 中心为O,P是的内切圆上一点,则( )A、 B、满足的点只有1个 C、 D、满足的点有2个
A、平面BEF B、直线与直线BF所成的角为 C、平面BEF与平面ABCD的夹角为 D、直线与平面ABCD所成的角为12. 已知正的边长为 , 中心为O,P是的内切圆上一点,则( )A、 B、满足的点只有1个 C、 D、满足的点有2个三、填空题
-
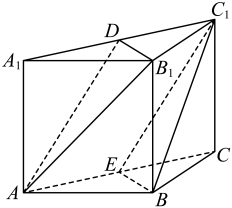
13. 已知复数满足 , 则.14. 若单位向量满足 , 且 , 则实数k的值为.15. 已知正方体的棱长为3,则到平面的距离为.16. 在中, , 是的角平分线,且交于点.若的面积为 , 则的最大值为.
四、解答题
-
17. 已知复数满足.(1)、求;(2)、求.18. 在中,角A,B,C的对边分别为a,b,c,且.(1)、求角A;(2)、若的面积为 , 求a的最小值.19. 如图所示,在中, , , , .
 (1)、试用向量 , 来表示 , ;(2)、若 , 求证:D,O,N三点共线.
(1)、试用向量 , 来表示 , ;(2)、若 , 求证:D,O,N三点共线.