安徽省示范高中培优联盟2022-2023学年高一下册春季联赛数学试卷

试卷更新日期：2023-06-26 类型：竞赛测试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 1 = 0}$ ， $B = {x | a x = 1}$ ，若 $A ∩ B = B$ ，则实数a取值集合为（）

A、 ${- 1}$ B、 ${1}$ C、 ${- 1 ， 1}$ D、 ${- 1 ， 0 ， 1}$

查看试题解析
2. “ $x = 2 k π + \frac{π}{3} (k \in Z)$ ”是“ $\tan x = \sqrt{3}$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 欧拉公式 $e^{i x} = c o s x + i s i n x$ （ $i$ 为虚数单位， $x ∈ R$ ）是由瑞土著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数之间的关系，根据此公式可知，下面结论中正确的是（）

A、 $e^{\frac{π}{2} i} - 1 = 0$ B、 $s i n x = \frac{e^{i x} - e^{- i x}}{2}$ C、 $e^{5 i}$ 在复平面内对应的点位于第二象限 D、 $(c o s x + i s i n x)^{2} = c o s 2 x + i s i n 2 x$

查看试题解析
4. 小明在整理数据时得到了该组数据的平均数为20，方差为28，后来发现有两个数据记录有误，一个错将11记录为21，另一个错将29记录为19.在对错误的数据进行更正后，重新求得该组数据的平均数为 $\bar{x}$ ，方差为 $s^{2}$ ，则（）

A、 $\bar{x} > 20$ ， $s^{2} < 28$ B、 $\bar{x} < 20$ ， $s^{2} > 28$ C、 $\bar{x} = 20$ ， $s^{2} < 28$ D、 $\bar{x} = 20$ ， $s^{2} > 28$

查看试题解析
5. 我国南宋著名数学家秦九韶在其著作《数书九章》中给出了三角形的面积公式：已知 $△ A B C$ 的三边分别为a，b，c，则 $△ A B C$ 的面积 $S = \sqrt{\frac{1}{4} [a^{2} c^{2} - {(\frac{a^{2} + c^{2} - b^{2}}{2})}^{2}]}$ .在 $△ A B C$ 中， $c = 6$ ， $a + b = 10$ ，则 $△ A B C$ 面积的最大值为（）

A、12 B、10 C、8 D、6

查看试题解析
6. 计算： $8 c o s^{2} 25 ° - t a n 40 ° - 4$ 的值为（）

A、1 B、 $\frac{\sqrt{3} - 1}{2}$ C、 $\frac{\sqrt{3} + 1}{2}$ D、 $\sqrt{3}$

查看试题解析
7. 已知平面向量 $\vec{a}$ 与 $\vec{a} + \vec{b}$ 的夹角为 $60 °$ ，若 $| \vec{a} | - t | \vec{b} | \leq 0$ 恒成立，则实数t的取值范围为（）

A、 $[\frac{2 \sqrt{3}}{3} ， + \infty)$ B、 $[\frac{\sqrt{3}}{2} ， + \infty)$ C、 $[2 ， + \infty)$ D、 $[\frac{1}{2} ， + \infty)$

查看试题解析
8. 已知函数 $f (x) = e^{x} - e^{1 - x} - a x$ ，若 $x_{1}$ ， $x_{2}$ 是函数 $g (x) = e^{x} + e^{1 - x} - a$ 的两个零点，且 $f (x_{1}) + f (x_{2}) = - 4$ ，则实数 $a =$ （）

A、2 B、3 C、4 D、5

查看试题解析
9. 已知 $a = 2^{2 l n 3}$ ， $b = 3^{3 l n 2}$ ， $c = 5^{l n 6}$ ，则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $a < c < b$ D、 $b < c < a$

查看试题解析

二、多选题

10. 为了得到函数 $g (x) = 2 s i n (8 x + \frac{3 π}{2})$ 的图象，只需把 $f (x) = 2 c o s 4 x$ 函数图象上所有点（）

A、向左平移 $\frac{π}{4}$ 个单位长度，再将横坐标缩短到原来的 $\frac{1}{2}$ 倍 B、向右平移 $\frac{π}{4}$ 个单位长度，再将横坐标缩短到原来的 $\frac{1}{2}$ 倍 C、横坐标伸长到原来的2倍，再向左平移 $\frac{π}{8}$ 个单位长度 D、横坐标缩短到原来的 $\frac{1}{2}$ 倍，再向左平移 $\frac{π}{8}$ 个单位长度

查看试题解析
11. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E ， F$ 分别为 $B C ， C C_{1}$ 的中点，则（）

A、直线 $A_{1} B$ 与 $E F$ 所成的角的大小为 $60 °$ B、直线 $A_{1} C ⊥$ 平面 $D E F$ C、平面 $D E F ⊥$ 平面 $B C C_{1} B_{1}$ D、平面 $D E F$ 将正方体截成的两部分的体积之比为 $23 ： 1$

查看试题解析
12. 一位植物学家想要研究某类植物生长1年之后的高度，他随机抽取了n株此类作物，测得它们生长1年之后的高度（单位：cm），将收集到的数据按照 $[30 ， 40)$ ， $[40 ， 50)$ ， $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ 分组，画出频率分布直方图，已知随机抽取的植物生长1年之后高度低于60cm的有20株，则以下结论中正确的是（）

A、 $n = 100$ B、此次检测植物生长高度的第80百分位数约为80 C、此次检测植物生长高度的众数的估计值为80 D、此次检测植物生长高度在 $[70 ， 90)$ 之间的有50株

查看试题解析

三、单选题

13. 已知 $f (x)$ 是定义在有限实数集A上的函数，且 $1 \in A$ ，若函数 $f (x)$ 的图象绕原点逆时针旋转 $3 0^{∘}$ 后与原图象重合，则 $f (1)$ 的值不可能是（）

A、0 B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析

四、多选题

14. 已知函数 $f (x)$ ， $g (x)$ 的定义域均为 $R$ ，且满足 $f (2 - x) + f (x) = 0$ ， $f (1 - x) + g (x) = 3$ ， $f (x) + g (x - 3) = 3$ ，则（）

A、 $f (x)$ 为奇函数 B、4为 $g (x)$ 的周期 C、 $f (1) + f (2) + \cdot \cdot \cdot + f (20) = 60$ D、 $g (1) + g (2) + \cdot \cdot \cdot + g (20) = 60$

查看试题解析

五、填空题

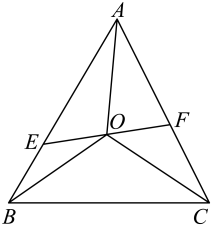
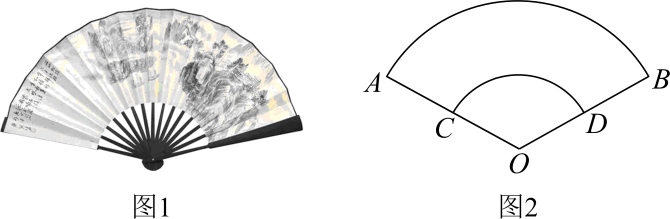
15. 已知函数 $f (x) = l o g_{a} (\sqrt{x^{2} + 3 a} - x)$ 是奇函数，则a的值为.

查看试题解析
16. 中国扇文化有着深厚的文化底蕴，是民族文化的一个组成部分，与竹文化、道教文化有着密切关系，历来中国有“制扇王国”之称.现有一块扇子如图1所示，其平面图如图2所示，在扇形中，已知 $∠ A O B = 120 °$ ， $O A = 6$ ， $O C = 2$ ，则扇面（曲边四边形ABCD）的面积为.

查看试题解析
17. 已知正数a，b满足 $l n \frac{2 - b}{a} = 2 a + 2 b - 4$ ，则 $\frac{1}{a} + \frac{2}{b} + \frac{2}{a b}$ 的最小值为.

查看试题解析
18. 已知函数 $y = f (x)$ ， $x ∈ A$ ，对任意的a，b， $c \in A$ ，都存在以 $f (a)$ ， $f (b)$ ， $f (c)$ 为三边的三角形，则称该函数为三角形函数.若函数 $f (x) = {\begin{array}{l} x + m ， 0 \leq x \leq \frac{3}{2} \\ x + \frac{1}{x - 1} ， \frac{3}{2} < x \leq 3 \end{array}$ 是三角形函数，则实数m的取值范围是.

查看试题解析

六、解答题

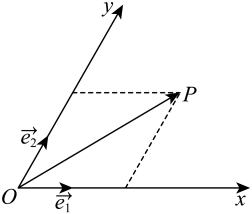
19. 如图，斜坐标系 $x O y$ 中， $\vec{e_{1}}$ ， $\vec{e_{2}}$ 分别是与 $x$ 轴， $y$ 轴正方向同向的单位向量，且 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 的夹角为 $60 °$ ，定义向量 $\vec{O P} = x \vec{e_{1}} + y \vec{e_{2}}$ 在斜坐标系 $x O y$ 中的坐标为有序数对 $(x ， y)$ ，在斜坐标系 $x O y$ 中完成下列问题：

(1)、若向量 $\vec{O P_{1}}$ ， $\vec{O P_{2}}$ 的坐标分别为 $(2 ， 3)$ ， $(3 ， 4)$ ，计算 $| \vec{P_{1} P_{2}} |$ 的大小；

(2)、已知向量 $\vec{O M}$ 的坐标为 $(x_{1} ， y_{1})$ ，向量 $\vec{O N}$ 的坐标为 $(x_{2} ， y_{2})$ ，证明：若 $\vec{O M} / / \vec{O N}$ ，则 $x_{1} y_{2} - x_{2} y_{1} = 0$ .

查看试题解析
20. 已知 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 在区间 $(- \frac{π}{8} ， \frac{3 π}{8})$ 上单调，满足 $f (0) = - \sqrt{2}$ ，对任意的 $x ∈ R$ ，都有 $| f (x) | \leq f (\frac{3 π}{8})$ .

(1)、求 $f (x)$ 的解析式；

(2)、设 $g (x) = f (x) c o s 2 x$ ，求 $g (x)$ 在 $(0 ， \frac{π}{2})$ 上单调递增区间.

查看试题解析
21. 在四面体 $P - A B C$ 中，点H为 $△ A B C$ 的垂心，且 $P H ⊥$ 平面 $A B C$ ．

(1)、若 $A P ⊥ P C$ ，求证： $P A ⊥ P B$ ；

(2)、若 $P B = A B$ ，证明： $P C = A C$ ．

查看试题解析

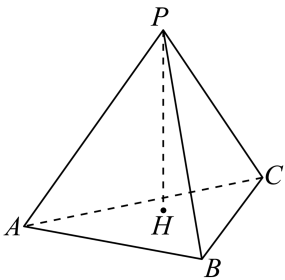22. 某学校需要从甲、乙两名学生中选一人参加全国高中数学竞赛，现整理了近期两人5次模拟考试的成绩，结果如下表：

	第一次	第二次	第三次	第四次	第五次
甲的成绩（分）	78	80	65	85	92
乙的成绩（分）	75	86	70	95	74

(1)、如果根据甲、乙两人近5次的考试成绩，你认为选谁参加较合适？并说明理由；

(2)、如果按照如下方案推荐参加全国高中数学竞赛：

方案一：每人从5道备选题中任意抽出1道，若答对，则可参加全国高中数学竞赛，否则被淘汰；

方案二：每人从5道备选题中任意抽出3道，若至少答对其中2道，则可参加全国高中数学竞赛，否则被淘汰.

已知学生甲只会5道备选题中的3道，那么学生甲选择哪种答题方案可参加全国高中数学竞赛的可能性更大？并说明理由.

查看试题解析

23. 已知函数 $f (x) = | x^{2} - k x - m |$ ， $k ， m \in R$ .

(1)、若 $m = 2 k^{2}$ ， $f (x)$ 在 $(1 ， + \infty)$ 上单调递增，求 $k$ 的取值范围；

(2)、对任意 $x \in [a ， b]$ ，都有 $f (x) ≤ 1$ ，证明： $b - a \leq 2 \sqrt{2}$ .

查看试题解析
24. 如图所示，已知 $△ A B C$ 的外接圆半径为 $r$ ， $E$ ， $F$ 是线段 $A B$ ， $A C$ 上的两点，点 $O$ 是 $△ A B C$ 的外心，且 $O$ 是线段 $E F$ 的中点， $O E = \frac{\sqrt{3}}{3} r$ .

(1)、证明： $A E \cdot E B = A F \cdot F C = \frac{2 r^{2}}{3}$ ；

(2)、求 $\frac{S_{△ A B C}}{S_{△ A E F}}$ 的最小值.

查看试题解析
25. 双曲函数是一类与三角函数类似的函数，在物理及生活中有着重要应用.称 $c o s h x = \frac{e^{x} + e^{- x}}{2}$ 为双曲余弦函数，称 $s i n h x = \frac{e^{x} - e^{- x}}{2}$ 为双曲正弦函数.

(1)、若关于x的不等式 $2 c o s h x + m e^{- x} - 1 - m \geq 0$ 在 $[l n 2 ， + \infty)$ 上恒成立，求实数m的取值范围；

(2)、函数 $f (x) = 2 m c o s h (2 x) - 2 s i n h (x) - 3$ 在 $x \in [0 ， l n 2]$ 有2个零点，求实数m的取值范围.

查看试题解析