安徽省示范高中培优联盟2022-2023学年高二下学期春季联赛数学试题

试卷更新日期：2023-06-26 类型：竞赛测试

进入出卷网下载

一、单选题

1. 已知集合 $P = {(x ， y) ∣ y = x^{2}} ， Q = {(x ， y) ∣ y = \sqrt{x}}$ ，则 $P ∩ Q =$ （）

A、 ${0}$ B、 ${0 ， 1}$ C、 ${(0 ， 0)}$ D、 ${(0 ， 0) ， (1 ， 1)}$

查看试题解析
2. 若 $1 + \sqrt{3} i$ 是关于 $x$ 的实系数方程 $a x^{2} + b x + 1 = 0$ 的一个复数根，则（）

A、 $a = \frac{1}{4}$ ， $b = \frac{1}{2}$ B、 $a = \frac{1}{4}$ ， $b = - \frac{1}{2}$ C、 $a = - \frac{1}{4}$ ， $b = \frac{1}{2}$ D、 $a = - \frac{1}{4}$ ， $b = - \frac{1}{2}$

查看试题解析
3. 已知 $α ， β$ 是空间两个不同的平面， $m ， n$ 是空间两条不同的直线，则下列命题为真命题的是（）

A、若 $m ∥ α ， n ∥ α$ ，则 $m ∥ n$ B、若 $m ∥ α ， m ∥ n$ ，则 $n ∥ α$ C、若 $m ⊥ α ， n ∥ β$ ，且 $m ⊥ n$ ，则 $α ⊥ β$ D、若 $m ⊥ α ， n ⊥ β$ ，且 $α ∥ β$ ，则 $m ∥ n$

查看试题解析
4. 某公司将包括2名女员工在内的5名员工派往3个不同的地方学习，要求每人去一个地方，每个地方至少去一人，则2名女员工必须在一起学习的不同的分配方案有（）

A、24 B、32 C、36 D、48

查看试题解析

5. 著名的天文学家拉普拉斯曾经说过“对数的发明以其节省劳力而延长了天文学家的寿命”，对数可以将乘除运算转化为加减运算，从而简化运算过程.在一次趣味表演中，主持人出题：一个35位整数的31次方根仍是一个整数，下面我报出这个35位数，请说出它的31次方根.还未等主持人报出第一个数字，速算专家已经写出了答案：这个数的31次方根是13，他的秘诀就是：他心中记住了下面的表（表中常用对数为近似值），请你也试一试，一个20位整数的32次方根仍是一个整数，这个32次方根是多少？（）

真数	常用对数	真数	常用对数
2	0.30	9	0.95
3	0.48	10	1.00
4	0.60	11	1.04
5	0.70	12	1.08
6	0.78	13	1.11
7	0.85	14	1.15
8	0.90	15	1.18

A、3 B、4 C、5 D、6

查看试题解析

6. 已知函数 $f (x) = x^{3} + a x^{2} + b x$ 有两个极值点 $x_{1} ， x_{2}$ ，且 $f (x_{1}) = x_{2}$ ， $f (x_{2}) = x_{1}$ ，那么关于 $x$ 的方程 $3 {[f (x)]}^{2} + 2 a f (x) + b = 0$ 的不同实根的个数是（）

A、6个 B、4个 C、2个 D、1个

查看试题解析
7. 已知矩形 $A B C D$ 中， $A B = 2 ， A D = 1$ ，沿着对角线 $A C$ 将 $△ A C D$ 折起，使得点 $D$ 不在平面 $A B C$ 内，当 $A D ⊥ B C$ 时，求该四面体 $A B C D$ 的内切球和外接球的表面积比值为（）

A、 $\frac{18 - 9 \sqrt{3}}{5}$ B、 $\frac{19 - 9 \sqrt{3}}{5}$ C、 $\frac{21 - 12 \sqrt{3}}{5}$ D、 $\frac{24 - 12 \sqrt{3}}{5}$

查看试题解析
8. 我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.请根据此方法求函数 $f (x ， y) = \sqrt{x^{2} - \sqrt{3} x + 1} + \sqrt{y^{2} - \sqrt{3} y + 1} + \sqrt{x^{2} - \sqrt{3} x y + y^{2}} (x > 0 ， y > 0)$ 的最小值（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析

二、多选题

9. 已知正方形 $A B C D$ 的边长为2，点 $M ， N$ 分别是线段 $C D ， B C$ 上的动点，若满足 $\vec{A C} = x \vec{A M} + y \vec{A N}$ ，则下列说法正确的是（）

A、当 $x = 1$ 时，则 $y = 1$ B、当 $x = y = \frac{2}{3}$ 时，点 $M ， N$ 分别是线段 $C D ， B C$ 的中点 C、当 $x = y = \frac{2}{3}$ 时， $\vec{A C} \cdot \vec{M N} = 0$ D、当 $\frac{1}{C M^{2}} + \frac{1}{C N^{2}} = 1$ 时， $x + y$ 的最小值为 $\frac{8 + 2 \sqrt{2}}{7}$

查看试题解析
10. 如图所示，已知 $O (0 ， 0)$ ， $A (2 ， 0)$ ， $B_{1} (1 ， 1)$ ，作以 $B_{1}$ 为直角顶点的等腰直角 $△ O A B_{1}$ ，作点 $A$ 和点 $B_{1}$ 的中点 $C_{1}$ ，继续作以 $C_{1}$ 为直角顶点的等腰直角 $△ B_{1} B_{2} C_{1} ， ⋯ ⋯$ ，如此继续作中点，作等腰直角三角形.这样会得到一组分别以 $B_{1} ， C_{1} ， B_{2} ， C_{2} ， ⋯ ⋯$ 为直角顶点的等腰直角三角形.下列说法正确的是（）

A、所作的等腰直角三角形的边长构成公比为 $\frac{1}{2}$ 的等比数列 B、第4个等腰直角三角形的不在第3个等腰直角三角形边上的顶点坐标为 $B_{3} (\frac{9}{4} ， 1)$ C、点 $C_{4}$ 的纵坐标为 $\frac{511}{512}$ D、若记第 $n$ 个等腰直角三角形的面积为 $S_{n}$ ，则 $\underset{n \to \infty}{l i m} \sum_{i = 1}^{n} S_{i} = \frac{4}{3}$

查看试题解析
11. 已知函数 $f (x) = \sqrt{3} c o s (ω x + \frac{π}{4}) + c o s (ω x - \frac{π}{4}) (ω > 0)$ ，当 $x \in [0 ， \frac{π}{2}]$ 时函数恰有3个零点，则正整数 $ω$ 的取值可以是（）

A、5 B、6 C、7 D、8

查看试题解析
12. 我们可以用统计图表表示数据，对获得数据进行统计分析.据《中国统计年鉴（2022）》可知，2016~2021年我国人口年龄分布情况（百分比）如表所示.（已知少儿抚养比 $(%) = \frac{0 \sim 14 岁人数}{15 \sim 64 岁人数} \times 100 %$ ，老年抚养比 $(%) = \frac{65 岁及以上人数}{15 \sim 64 岁人数} \times 100 %$ ，总抚养比（%） $=$ 少儿抚养比（%）+老年抚养比（%））根据图表，

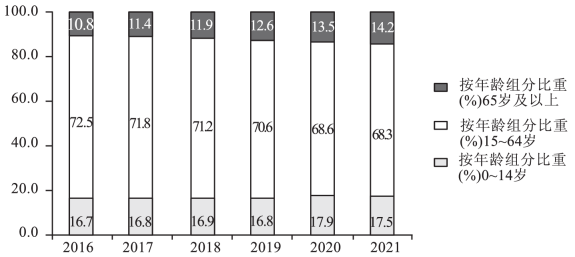
下列说法正确的有（）

A、从2016年到2021年期间，0~14岁人口比重在逐年上升 B、从2016年到2021年期间，15~64岁人口比重在逐年下降 C、2021赡养老人的压力比2020年更重 D、2021年总抚养比大于2020年总抚养比

查看试题解析

三、填空题

13. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点为 $F$ ，在双曲线左支上取一点 $M$ ，若直线 $M F$ 与以双曲线实轴为直径的圆相切于 $N$ ，若向量 $\vec{M N} = 2 \vec{N F}$ ，则双曲线 $C$ 的离心率为.

查看试题解析
14. 已知函数 $y = f (x)$ 定义域为 $R$ 且满足① $y = f (x + 2)$ 为偶函数；②任意 $x \geq 2 ， y \geq 2$ 都有 $f (x + y) - 1 = f (x) + f (y)$ 成立；③ $\forall x_{1} ， x_{2} ∈ [2 ， + \infty) ， x_{1} \neq x_{2}$ ，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > 0$ ，请给出满足上述三个性质的一个函数为.

查看试题解析
15. 若 $(10 x + 6 y)^{3} = a x^{3} + b x^{2} y + c x y^{2} + d y^{3}$ ，则 $- a + 2 b - 4 c + 8 d =$ .

查看试题解析
16. 已知 $x^{2} + y^{2} - 8 x - 6 y + 16 = 0$ ，则 $\frac{y}{x}$ 的最小值为.

查看试题解析

四、解答题

17. 已知 $f (x) = l n (x - 1) + a x (a \in R)$

(1)、讨论函数 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时， $b e^{x} + l n b + x + 1 \geq f (x)$ 恒成立，求 $b$ 的取值范围.

查看试题解析
18. 已知双曲线的标准方程为 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ，其中点 $F$ 为右焦点，过点 $F$ 作垂直于 $x$ 轴的垂线，在第一象限与双曲线相交于点 $A$ ，过点 $F$ 作双曲线渐近线的垂线，垂足为 $M$ ，若 $A F = 6$ ， $M F = 2 \sqrt{3}$ .

(1)、求双曲线的标准方程；

(2)、过点 $M$ 作 $A F$ 的平行线 $l$ ，在直线 $l$ 上任取一点 $P$ ，连接 $P A$ 与双曲线相交于点 $B$ ，求证点 $P$ 到直线 $B F$ 的距离是定值.

查看试题解析
19. 如图所示，在四棱锥 $S - A B C D$ 中，侧面 $S A B$ 为边长为2的等边三角形，底面 $A B C D$ 为等腰梯形， $A B / / C D$ ， $C D = 1$ ，底面梯形的两条对角线 $A C$ 和 $B D$ 互相垂直，垂足为 $O$ ， $S O = \sqrt{2}$ ，点 $M$ 为棱 $S B$ 上的任意一点.

(1)、求证： $A C ⊥ D M$ ；

(2)、是否存在点 $M$ 使得二面角 $M - A D - C$ 的余弦值为 $\frac{7 \sqrt{6}}{18}$ ，若存在求出点 $M$ 的位置；若不存在请说明理由.

查看试题解析
20. “十三五”时期，在党中央､国务院坚强领导下，全民健身国家战略深入实施，全民健身公共服务水平显著提升，全民健身场地设施逐步增多，人民群众通过健身促进健康的热情日益高涨，经常参加体育锻炼人数和参加锻炼的时间都在明显增加.某城市为了调查该市市民积极参加体育锻炼的情况，从市民中随机抽取了50人，结果是他们参加锻炼的时间都在区间 $[50 ， 100]$ 内，锻炼时间的频率分布直方图如下：

(1)、如果锻炼时间的中位数的估计值大于或者等于平均数的估计值，则说明该城市市民积极参加锻炼的意识很强，否则说明该城市市民积极参加锻炼的意识不强，请你根据直方图对他们积极参加锻炼的意识强与不强做出判断；

(2)、假如根据调查统计结果规定：锻炼时间在 $[80 ， 100]$ 的市民为优秀层次，时间在 $[50 ， 80)$ 的为非优秀层次，
（ⅰ）从被调查的50人中按分层抽样的方法抽取10人，再从这10人中随机抽取5人，求这5人中优秀层次的人数大于非优秀层次的人数的概率；

（ⅱ）用频率作为概率，现从该城市所有市民中随机抽取3人，这3人中锻炼时间为优秀层次的人数为X，求随机变量X的分布列和数学期望.

查看试题解析
21. 如下图，已知有 $n^{2} (n \geq 4)$ 个正数排成 $n$ 行 $n$ 列：其中每一行都成等差数列，每一列都成等比数列，且所有的公比相等，已知 $a_{12} = 1$ ， $a_{14} = 2$ ， $a_{42} = 8$ .

(1)、求 $a_{34}$ 和 $a_{44}$ 的值；

(2)、求 $S = a_{11} + a_{22} + ⋯ + a_{n n}$ （用含 $n$ 的式子表达）.

查看试题解析
22. 已知 $△ A B C$ 的三个内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，且 $A = \frac{π}{3}$ ， $b c o s^{2} \frac{C}{2} + c c o s^{2} \frac{B}{2} = \frac{b + c}{2} + \sqrt{3}$ ，设 $B = x$ ， $△ A B C$ 的周长为 $y$ .

(1)、当 $x = \frac{π}{4}$ 时，求 $y$ 的值；

(2)、求函数 $y = f (x)$ 的解析式及最大值.

查看试题解析