河南省2023年初中数学学业水平测试
试卷更新日期:2023-06-26 类型:中考模拟
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个正确的。
-
1. 的绝对值是( )A、 B、 C、 D、2. 2023全国“两会”政府工作报告中指出:我国粮食产量连年稳定在1.3万亿斤以上.其中数据“1.3万亿”用科学记数法可表示为( )A、 B、 C、 D、3. 某几何体的三视图如图所示,这个几何体是( )
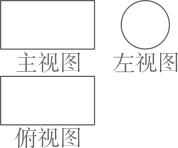 A、
A、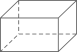 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在中,作边AB的垂直平分线,交边BC于点 , 连接AD.若 , 则的度数为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在中,作边AB的垂直平分线,交边BC于点 , 连接AD.若 , 则的度数为( )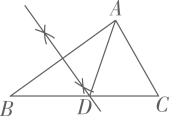 A、50° B、40° C、35° D、30°6. 把不等式组的解集表示在数轴上,下列选项正确的是( )A、
A、50° B、40° C、35° D、30°6. 把不等式组的解集表示在数轴上,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 若关于的一元二次方程有两个不相等的实数根,则的值可以是( )A、-3 B、-2 C、0 D、-18. 近年来我国航天事业取得了一系列的伟大成就,现有5张卡片正面图案如图所示,它们除此之外其他完全相同,把这5张卡片背面朝上洗匀,从中随机抽取两张卡片正面图案恰好是“嫦娥五号”和“卫星导航系统”的概率是( )
7. 若关于的一元二次方程有两个不相等的实数根,则的值可以是( )A、-3 B、-2 C、0 D、-18. 近年来我国航天事业取得了一系列的伟大成就,现有5张卡片正面图案如图所示,它们除此之外其他完全相同,把这5张卡片背面朝上洗匀,从中随机抽取两张卡片正面图案恰好是“嫦娥五号”和“卫星导航系统”的概率是( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形OABC的顶点在原点上,OA边在轴的正半轴上,轴, , 将四边形OABC绕点送时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,四边形OABC的顶点在原点上,OA边在轴的正半轴上,轴, , 将四边形OABC绕点送时针旋转,每次旋转 , 则第2023次旋转结束时,点的坐标为( ) A、 B、 C、 D、10. 如图1,在矩形ABCD中,动点从点出发沿方向运动到点停止,动点从点出发沿方向运动到点停止,若点P,Q同时出发,点的速度为 , 点的速度为 , 设运动时间为与的函数关系图象如图2所示,则AC的长为( )
A、 B、 C、 D、10. 如图1,在矩形ABCD中,动点从点出发沿方向运动到点停止,动点从点出发沿方向运动到点停止,若点P,Q同时出发,点的速度为 , 点的速度为 , 设运动时间为与的函数关系图象如图2所示,则AC的长为( ) A、8 B、9 C、10 D、14
A、8 B、9 C、10 D、14二、填空题(每小题3分,共15分)
-
11. 某种试剂的说明书上标明保存温度是 , 请你写出一个适合该试剂保存的温度:℃.12. 已知点在直线上,且 , 则的取值范围是.13. 某校计划从小颖、小亮、小东、小朋四名学生中选拔一人参加全市知识竞赛,下表是他们最近3次选拔测试的平均成绩及方差:
小颖
小亮
小东
小明
平均成绩/分
97
96
95
97
方差
0.35
0.42
0.36
0.15
学校决定依据他们的平均成绩及稳定性进行选拔,那么被选中的学生应是.
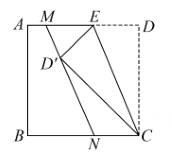
14. 如图,在扇形中,分别是OA,OB的中点,连接AD和BC交于点 , 若 , 则图中阴影部分的面积为. 15. 如图,正方形ABCD的边长为5,E是边AD上的一动点,将正方形沿CE翻折,点的对应点为 , 过点作折痕CE的平行线,分别交正方形ABCD的边于点M,N(点M在点上方),若 , 则DE的长为.
15. 如图,正方形ABCD的边长为5,E是边AD上的一动点,将正方形沿CE翻折,点的对应点为 , 过点作折痕CE的平行线,分别交正方形ABCD的边于点M,N(点M在点上方),若 , 则DE的长为.
三、解答题(本大题共8个小题,共75分)
-
16.(1)、计算:(2)、化简:17. 互联网已成为当代未成年人重要的学习、社交、娱乐工具,对其成长产生深刻影响.2022年11月30日,共青团中央维护青少年权益部、中国互联网络信息中心(CNNIC)、中国青少年新媒体协会联合发布了《2021年全国米成年人互联网使用情况研究报告》(注:此报告中未成年网民指6岁到18岁的在校学生中的网民).根据报告中的数据,得到以下两幅统计图:
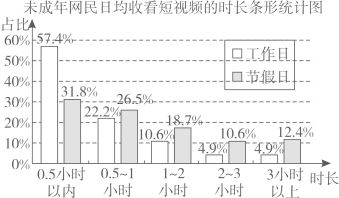

根据以上信息解答下列问题:
(1)、未成年网民假日收看短视频时长的中位数在范围内,未成年网民收看短视频的内容题材最多的是类。(2)、若从全国6岁到18岁的在校生中随机抽取1000人,请分别估计其中工作日和节假日收看短视频的时长在1小时及以上的学生人数。(3)、某班为举办“健康上网”的主题班会,从以上统计图中获取了一些信息,请你写出一条获得的信息,并就此提出一条合理的建议。18. 文昌阁位于河南省辉县市区,创建于明代,为八角形三层攒尖顶阁楼,砖木结构.文昌阁是河南省第五批文物保护单位,其建筑结构严谨,造型精巧,工艺精致,气势宏伟,体量高大,是明代木构阁楼建筑的精华,具有重要的历史、科学、艺术价值.某数学兴趣小组准备测量文昌阁阁身的高度,为此制订了测量方案,并利用周末完成了测量,测量结果如下表:活动课题
测量文昌阁阁身的高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
示意图

测量步骤
如上图:①利用测角仪在台阶D处测得文昌阁顶点A的仰角为45°;
②利用测角仪在台阶C处测得的文昌阁顶点A的仰角为57°;
③利用皮尺测量每个台阶的高度计算出两处台阶的高度均为1.8m(即点B和点C,点C和点D的垂直距离均为1.8m),利用皮尺测量每个台阶的宽度及点C和点D到台阶边缘的距离计算出点C和点D的水平距离为6.6m(已知A、B、C、D、E均在同一平面内)
请运用所学知识,根据上表中的数据,计算文昌阁阁身AB的高度。(结果取整数.参考数据:sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
19. 某科技小组的同学制作了一个简易台秤(如图1)用来测物体的质量,内部电路如图2所示,其中电流表的表盘被改装为台秤的示数.已知电源电压U为18V,定值电阻R0为30Ω,电阻R为力敏电阻,其阻值R(Ω)与所受压力F(N)符合反比例函数关系.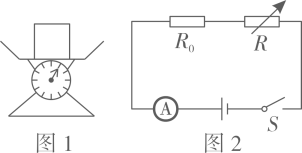 (1)、请补全下面的表格,在图3中补全点,画出R(Ω)与F(N)的关系图象,并写出阻R(Ω)与压力F(N)的函数关系式.
(1)、请补全下面的表格,在图3中补全点,画出R(Ω)与F(N)的关系图象,并写出阻R(Ω)与压力F(N)的函数关系式.F(N)
120
▲
60
50
▲
30
R(Ω)
5
6
I0
12
15
20
 (2)、已知电路中电流与电阻、电源电压的关系式 , 当电流表的示数达到最大值时,台秤达到量程的最大值.若电流表的量程为 , 则该台秤最大可称多重的物体?(3)、已知力敏电阻受压力与所测物体的质量的关系为.若力敏电阻阻值的变化范围为 , 则所测物体的质量的变化范围是.20. 国家"双減"政策实施后,某校开展了丰富多彩的社团活动,其中部分同学报名参加了中国象棋和围棋两个社团,该校为参加社团的同学去商场购买中国象棋和围棋.已知购买5副中国象棋和3副围棋共花费165元,购买4副中国象棋和6副围棋共花费240元.(1)、求每副中国象棋和围棋的价格各是多少元。(2)、在购买时,恰逢商场推出了优惠活动,活动的方案如下:
(2)、已知电路中电流与电阻、电源电压的关系式 , 当电流表的示数达到最大值时,台秤达到量程的最大值.若电流表的量程为 , 则该台秤最大可称多重的物体?(3)、已知力敏电阻受压力与所测物体的质量的关系为.若力敏电阻阻值的变化范围为 , 则所测物体的质量的变化范围是.20. 国家"双減"政策实施后,某校开展了丰富多彩的社团活动,其中部分同学报名参加了中国象棋和围棋两个社团,该校为参加社团的同学去商场购买中国象棋和围棋.已知购买5副中国象棋和3副围棋共花费165元,购买4副中国象棋和6副围棋共花费240元.(1)、求每副中国象棋和围棋的价格各是多少元。(2)、在购买时,恰逢商场推出了优惠活动,活动的方案如下:方案一:购买围棋不超过20副时,围棋和中国象棋均按原价付款;超过20副时,超过的部分每购买1副围棋赠送1副中国象棋;
方案二:按购买总金额的八折付款.
若该校共需购买40副围棋和副中国象棋,请通过计算说明该校选择哪种方案更划算.
21. 如图,在平面直角坐标系xOy中,拋物线的顶点为 , 交轴于点 , 点是拋物线上一点.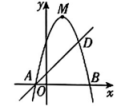 (1)、求抛物线的表达式及顶点的坐标.(2)、当时,求二次函数的最大值与最小值的差.(3)、若点是轴上方抛物线上的点(不与点A,B,D重合),设点P的横坐标为 , 过点作轴,交直线AD于点 , 当线段PQ的长随的增大而增大时,请直接写出的取值范围.22. 中国是世界上机械发展最早的国家之一.如图1是一辆明代的运输板车,该车沿用宋元制式和包繁式结构,车身选材厚重、纹理精美,低重心的物理结构兼顾了承重性和安全性.如图2是板车侧面的部分示意图,AB为车轮的直径,过圆心O的车架AC一端点着地时,地面CD与车轮相切于点 , 连接AD,BD.
(1)、求抛物线的表达式及顶点的坐标.(2)、当时,求二次函数的最大值与最小值的差.(3)、若点是轴上方抛物线上的点(不与点A,B,D重合),设点P的横坐标为 , 过点作轴,交直线AD于点 , 当线段PQ的长随的增大而增大时,请直接写出的取值范围.22. 中国是世界上机械发展最早的国家之一.如图1是一辆明代的运输板车,该车沿用宋元制式和包繁式结构,车身选材厚重、纹理精美,低重心的物理结构兼顾了承重性和安全性.如图2是板车侧面的部分示意图,AB为车轮的直径,过圆心O的车架AC一端点着地时,地面CD与车轮相切于点 , 连接AD,BD.
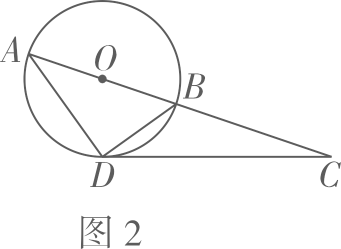 (1)、求证:∠ADC=∠DBC.(2)、若测得 , 求AD的长。23. 综合与实践
(1)、求证:∠ADC=∠DBC.(2)、若测得 , 求AD的长。23. 综合与实践【问题情境】数学活动课上,老师给出了这样一个问题:
如图1,在中, , 射线AD平分 , 将射线AD绕点逆时针旋转 , 得到射线 , 在射线上取点 , 使得 , 连接BE分别交AD,AC于点M,N,连接CE.问:之间的数量关系是什么?线段DM,CN之间的数量关系是什么?

【特例探究】“勤奋”小组的同学们先将问题特殊化,探究过程如下:
甲同学:当时,如图2,通过探究可以发现,都是等腰三角形;
乙同学:可以证明 , 得到;
丙同学:过点做 , 垂足为 , 如图3,则;
丁同学:可以证明 , 则 , …
(1)、根据以上探究过程,得出结论:①之间的数量关系是;
②线段DM,CN之间的数量关系是.
(2)、【类比探究】“智慧”小组的同学们在“勤奋”小组的基础上,进一步探究一般情形,当时,如图1,⑴中的两个结论是否仍然成立?如果成立,请仅就图1的情形进行证明;如果不成立,请说明理由。
(3)、【迁移应用】“创新”小组的同学们改变了条件,当时,如图4,若射线AD是的三等分角线, , 其他条件不变,请直接写出MN的长.
