湖北省十堰市2023年中考数学试卷
试卷更新日期:2023-06-26 类型:中考真卷
一、选择题(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.
-
1. 的倒数是( )A、 B、 C、 D、2. 下列几何体中,三视图的三个视图完全相同的几何体是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 任意掷一枚均匀的小正方体色子,朝上点数是偶数的概率为( )A、 B、 C、 D、5. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 任意掷一枚均匀的小正方体色子,朝上点数是偶数的概率为( )A、 B、 C、 D、5. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( ) A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变6. 为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )A、 B、 C、 D、7. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( )
A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变6. 为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )A、 B、 C、 D、7. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( ) A、米 B、米 C、米 D、米8. 如图,已知点C为圆锥母线的中点,为底面圆的直径, , , 一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为( )
A、米 B、米 C、米 D、米8. 如图,已知点C为圆锥母线的中点,为底面圆的直径, , , 一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为( )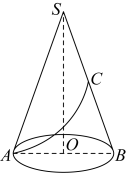 A、5 B、 C、 D、9. 如图,是的外接圆,弦交于点E, , , 过点O作于点F,延长交于点G,若 , , 则的长为( )
A、5 B、 C、 D、9. 如图,是的外接圆,弦交于点E, , , 过点O作于点F,延长交于点G,若 , , 则的长为( )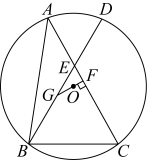 A、 B、7 C、8 D、10. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、
A、 B、7 C、8 D、10. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、二、填空题(本题有6个小题,每小题3分,共18分)
-
11. 2023年5月30日上午,我国载人航天飞船“神舟十六号”发射圆满成功,与此同时,中国载人航天办公室也宣布计划在2030年前实现中国人首次登陆距地球平均距离为万千米的月球,将用科学记数法表示为 .12. 若 , , 则的值是 .13. 一副三角板按如图所示放置,点A在上,点F在上,若 , 则°.
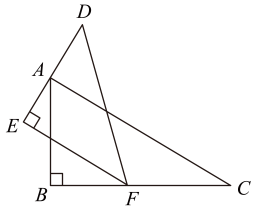 14. 用火柴棍拼成如下图案,其中第①个图案由4个小等边三角形围成1个小菱形,第②个图案由6个小等边三角形围成2个小菱形,……,若按此规律拼下去,则第n个图案需要火柴棍的根数为(用含n的式子表示).
14. 用火柴棍拼成如下图案,其中第①个图案由4个小等边三角形围成1个小菱形,第②个图案由6个小等边三角形围成2个小菱形,……,若按此规律拼下去,则第n个图案需要火柴棍的根数为(用含n的式子表示).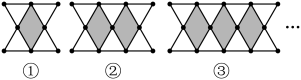 15. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 .
15. 如图,在菱形中,点E,F,G,H分别是 , , , 上的点,且 , 若菱形的面积等于24, , 则 . 16. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .
16. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .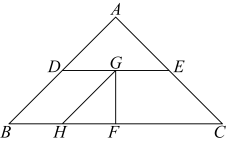
三、解答题(本题有9个小题,共72分)
-
17. 计算: .18. 化简: .19. 市体育局对甲、乙两运动队的某体育项目进行测试,两队人数相等,测试后统计队员的成绩分别为:7分、8分、9分、10分(满分为10分).依据测试成绩绘制了如图所示尚不完整的统计图表:
甲队成绩统计表
成绩
7分
8分
9分
10分
人数
0
1
m
7

请根据图表信息解答下列问题:
(1)、填空: , ;(2)、补齐乙队成绩条形统计图;(3)、①甲队成绩中位数为 ▲ , 乙队成绩的中位数为 ▲ ;②分别计算甲、乙两队成绩的平均数,并从中位数和平均数的角度分析哪个运动队的成绩较好.
20. 如图,的对角线交于点 , 分别以点为圆心,长为半径画弧,两弧交于点 , 连接 . (1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?21. 函数的图象可以由函数的图象左右平移得到.(1)、将函数的图象向右平移4个单位得到函数的图象,则;(2)、下列关于函数的性质:①图象关于点对称;②随的增大而减小;③图象关于直线对称;④的取值范围为 . 其中说法正确的是(填写序号);(3)、根据(1)中的值,写出不等式的解集: .22. 如图,在中, , 点在上,以为圆心,为半径的半圆分别交 , 于点 , 且点是弧的中点.
(1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?21. 函数的图象可以由函数的图象左右平移得到.(1)、将函数的图象向右平移4个单位得到函数的图象,则;(2)、下列关于函数的性质:①图象关于点对称;②随的增大而减小;③图象关于直线对称;④的取值范围为 . 其中说法正确的是(填写序号);(3)、根据(1)中的值,写出不等式的解集: .22. 如图,在中, , 点在上,以为圆心,为半径的半圆分别交 , 于点 , 且点是弧的中点. (1)、求证:是的切线;(2)、若 , 求图中阴影部分的面积(结果保留).23. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.24. 过正方形的顶点作直线 , 点关于直线的对称点为点 , 连接 , 直线交直线于点 .
(1)、求证:是的切线;(2)、若 , 求图中阴影部分的面积(结果保留).23. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.24. 过正方形的顶点作直线 , 点关于直线的对称点为点 , 连接 , 直线交直线于点 . (1)、如图1,若 , 则°;(2)、如图1,请探究线段 , , 之间的数量关系,并证明你的结论;(3)、在绕点转动的过程中,设 , 请直接用含的式子表示的长.25. 已知抛物线过点和点 , 与轴交于点 .
(1)、如图1,若 , 则°;(2)、如图1,请探究线段 , , 之间的数量关系,并证明你的结论;(3)、在绕点转动的过程中,设 , 请直接用含的式子表示的长.25. 已知抛物线过点和点 , 与轴交于点 . (1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.
(1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.