湖北省武汉市2023年中考数学试卷
试卷更新日期:2023-06-26 类型:中考真卷
一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
-
1. 实数3的相反数是( )A、3 B、 C、 D、2. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 掷两枚质地均匀的骰子,下列事件是随机事件的是( )A、点数的和为1 B、点数的和为6 C、点数的和大于12 D、点数的和小于134. 计算的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的左视图是( )
3. 掷两枚质地均匀的骰子,下列事件是随机事件的是( )A、点数的和为1 B、点数的和为6 C、点数的和大于12 D、点数的和小于134. 计算的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的左视图是( ) A、
A、 B、
B、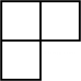 C、
C、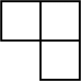 D、
D、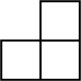 6. 关于反比例函数 , 下列结论正确的是( )A、图像位于第二、四象限 B、图像与坐标轴有公共点 C、图像所在的每一个象限内,随的增大而减小 D、图像经过点 , 则7. 某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )A、 B、 C、 D、8. 已知 , 计算的值是( )A、1 B、 C、2 D、9. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )
6. 关于反比例函数 , 下列结论正确的是( )A、图像位于第二、四象限 B、图像与坐标轴有公共点 C、图像所在的每一个象限内,随的增大而减小 D、图像经过点 , 则7. 某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )A、 B、 C、 D、8. 已知 , 计算的值是( )A、1 B、 C、2 D、9. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )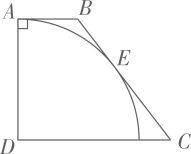 A、 B、 C、 D、10. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、285
A、 B、 C、 D、10. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、285二、填空题(共6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
-
11. 写出一个小于4的正无理数是 .12. 新时代十年来,我国建成世界上规模最大的社会保障体系.其中基本医疗保险的参保人数由5.4亿增加到13.6亿,参保率稳定在95%.将数据13.6亿用科学记数法表示为的形式,则的值是(备注:1亿=100000000).13. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm
(结果精确到0.1cm,参考数据: , , )
 14. 我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”如图是善行者与不善行者行走路程(单位:步)关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 .
14. 我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”如图是善行者与不善行者行走路程(单位:步)关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 . 15. 抛物线(是常数,)经过三点,且 . 下列四个结论:
15. 抛物线(是常数,)经过三点,且 . 下列四个结论:①;
②;
③当时,若点在该抛物线上,则;
④若关于的一元二次方程有两个相等的实数根,则 .
其中正确的是(填写序号).
16. 如图,平分等边的面积,折叠得到分别与相交于两点.若 , 用含的式子表示的长是 .
三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
-
17. 解不等式组请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集是 .18. 如图,在四边形中, , 点在的延长线上,连接 .
(4)、原不等式组的解集是 .18. 如图,在四边形中, , 点在的延长线上,连接 . (1)、求证:;(2)、若平分 , 直接写出的形状.19. 某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个休息日做家务的劳动时间(单位:)作为样本,将收集的数据整理后分为五个组别,其中A组的数据分别为:0.5,0.4,0.4,0.4,0.3,绘制成如下不完整的统计图表.
(1)、求证:;(2)、若平分 , 直接写出的形状.19. 某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个休息日做家务的劳动时间(单位:)作为样本,将收集的数据整理后分为五个组别,其中A组的数据分别为:0.5,0.4,0.4,0.4,0.3,绘制成如下不完整的统计图表.各组劳动时间的频数分布表
组别
时间
频数
5
20
15
8
各组劳动时间的扇形统计图
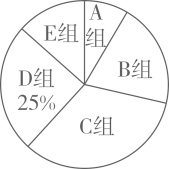
请根据以上信息解答下列问题.
(1)、A组数据的众数是;(2)、本次调查的样本容量是 , B组所在扇形的圆心角的大小是;(3)、若该校有名学生,估计该校学生劳动时间超过的人数.20. 如图,都是的半径, . (1)、求证:;(2)、若 , 求的半径.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、求证:;(2)、若 , 求的半径.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.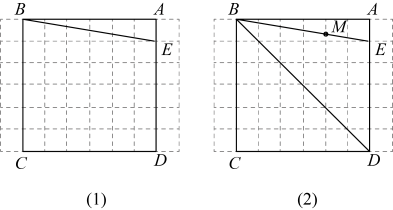 (1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .22. 某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.
(1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .22. 某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.飞行时间
0
2
4
6
8
…
飞行水平距离
0
10
20
30
40
…
飞行高度
0
22
40
54
64
…
探究发现:与 , 与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
 (1)、若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;(2)、在安全线上设置回收区域 . 若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.23. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , 交于点 , 探究与的数量关系.
(1)、若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;(2)、在安全线上设置回收区域 . 若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.23. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , 交于点 , 探究与的数量关系.
 (1)、问题探究:
(1)、问题探究:
先将问题特殊化,如图(2),当时,直接写出的大小;(2)、再探究一般情形,如图(1),求与的数量关系.问题拓展:
(3)、将图(1)特殊化,如图(3),当时,若 , 求的值.24. 抛物线交轴于两点(在的左边),交轴于点 .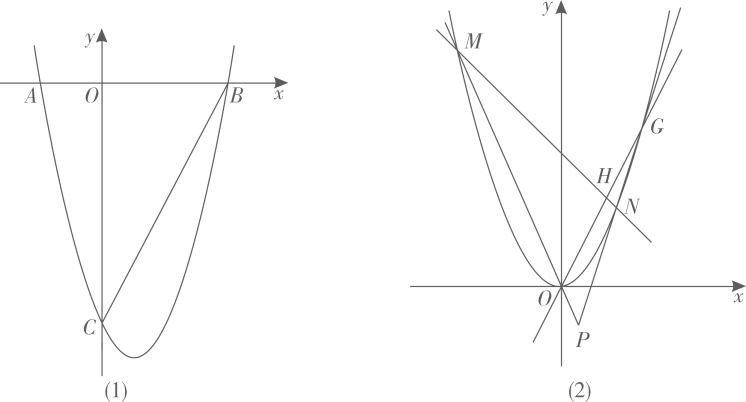 (1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.
(1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.