湖北省宜昌市2023年中考数学试卷
试卷更新日期:2023-06-26 类型:中考真卷
一、选择题(下列各题中,只有一个选项是符合题目要求的,请在答题卡上指定的位置填涂符合要求的选项前面的字母代号.每题3分,计33分.)
-
1. 下列运算正确的个数是( ).
①;②;③;④ .
A、4 B、3 C、2 D、12. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、 B、
B、 C、
C、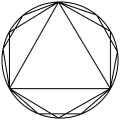 D、
D、 3. “五一”假期,宜昌旅游市场接待游客万人次,实现旅游总收入亿元.数据“亿”用科学记数法表示为( ).A、 B、 C、 D、4. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ).
3. “五一”假期,宜昌旅游市场接待游客万人次,实现旅游总收入亿元.数据“亿”用科学记数法表示为( ).A、 B、 C、 D、4. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ). A、文 B、明 C、典 D、范5. 如图,都是的半径,交于点D.若 , 则的长为( ).
A、文 B、明 C、典 D、范5. 如图,都是的半径,交于点D.若 , 则的长为( ). A、5 B、4 C、3 D、26. 下列运算正确的是( ).A、 B、 C、 D、7. 某反比例函数图象上四个点的坐标分别为 , 则,的大小关系为( )A、 B、 C、 D、8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ).
A、5 B、4 C、3 D、26. 下列运算正确的是( ).A、 B、 C、 D、7. 某反比例函数图象上四个点的坐标分别为 , 则,的大小关系为( )A、 B、 C、 D、8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ). A、 B、 C、 D、9. 在日历上,某些数满足一定的规律.如图是某年8月份的日历,任意选择其中所示的含4个数字的方框部分,设右上角的数字为a,则下列叙述中正确的是( ).
A、 B、 C、 D、9. 在日历上,某些数满足一定的规律.如图是某年8月份的日历,任意选择其中所示的含4个数字的方框部分,设右上角的数字为a,则下列叙述中正确的是( ).日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
A、左上角的数字为 B、左下角的数字为 C、右下角的数字为 D、方框中4个位置的数相加,结果是4的倍数10. 解不等式 , 下列在数轴上表示的解集正确的是( ).A、 B、
B、 C、
C、 D、
D、 11. 某校学生去距离学校的博物馆参观,一部分学生骑自行车先走,过了后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,汽车的速度是( ).A、 B、 C、 D、
11. 某校学生去距离学校的博物馆参观,一部分学生骑自行车先走,过了后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,汽车的速度是( ).A、 B、 C、 D、二、填空题(将答案写在答题卡上指定的位置.每题3分,计12分.)
-
12. 如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕 , 小宇测得长边 , 则四边形的周长为 .
 13. 如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的距离m.
13. 如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的距离m. 14. 已知、是方程的两根,则代数式的值为 .15. 如图,条形图描述了某车间工人日加工零件数的情况.这些工人日加工零件数的中位数是 .
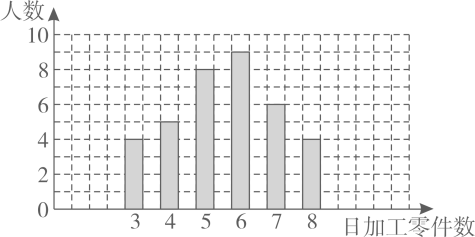
14. 已知、是方程的两根,则代数式的值为 .15. 如图,条形图描述了某车间工人日加工零件数的情况.这些工人日加工零件数的中位数是 .
三、解答题(将解答过程写在答题卡上指定的位置.本大题共有9题,计75分.)
-
16. 先化简,再求值: , 其中 .17. 如图,在方格纸中按要求画图,并完成填空.
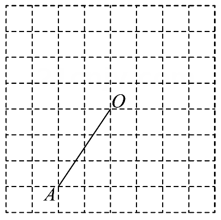
⑴画出线段绕点O顺时针旋转后得到的线段 , 连接;
⑵画出与关于直线对称的图形,点A的对称点是C;
⑶填空:的度数为 ▲ .
18. 某食用油的沸点温度远高于水的沸点温度.小聪想用刻度不超过的温度计测算出这种食用油沸点的温度.在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔测量一次锅中油温,得到的数据记录如下:时间t/s
0
10
20
30
40
油温y/
10
30
50
70
90
 (1)、小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温y(单位:)与加热的时间t(单位:s)符合初中学习过的某种函数关系,填空:可能是函数关系(请选填“正比例”“一次”“二次”“反比例”);(2)、根据以上判断,求y关于t的函数解析式;(3)、当加热时,油沸腾了,请推算沸点的温度.19. 2023年5月30日,“神舟十六号”航天飞船成功发射.如图,飞船在离地球大约的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在中, .
(1)、小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温y(单位:)与加热的时间t(单位:s)符合初中学习过的某种函数关系,填空:可能是函数关系(请选填“正比例”“一次”“二次”“反比例”);(2)、根据以上判断,求y关于t的函数解析式;(3)、当加热时,油沸腾了,请推算沸点的温度.19. 2023年5月30日,“神舟十六号”航天飞船成功发射.如图,飞船在离地球大约的圆形轨道上,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在中, .(参考数据:)
 (1)、求的值(精确到);(2)、在中,求的长(结果取整数).20. “阅读新时代,书香满宜昌”.在“全民阅读月”活动中,某校提供了四类适合学生阅读的书籍:A文学类,B科幻类,C漫画类,D数理类.为了解学生阅读兴趣,学校随机抽取了部分学生进行调查(每位学生仅选一类).根据收集到的数据,整理后得到下列不完整的图表:
(1)、求的值(精确到);(2)、在中,求的长(结果取整数).20. “阅读新时代,书香满宜昌”.在“全民阅读月”活动中,某校提供了四类适合学生阅读的书籍:A文学类,B科幻类,C漫画类,D数理类.为了解学生阅读兴趣,学校随机抽取了部分学生进行调查(每位学生仅选一类).根据收集到的数据,整理后得到下列不完整的图表:书籍类别 学生人数 A文学类 24 B科幻类 m C漫画类 16 D数理类 8 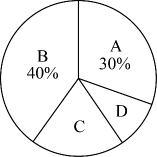 (1)、本次抽查的学生人数是 , 统计表中的;(2)、在扇形统计图中,“C漫画类”对应的圆心角的度数是;(3)、若该校共有1200名学生,请你估计该校学生选择“D数理类”书籍的学生人数;(4)、学校决定成立“文学”“科幻”“漫画”“数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率.21. 如图1,已知是的直径,是的切线,交于点 , .
(1)、本次抽查的学生人数是 , 统计表中的;(2)、在扇形统计图中,“C漫画类”对应的圆心角的度数是;(3)、若该校共有1200名学生,请你估计该校学生选择“D数理类”书籍的学生人数;(4)、学校决定成立“文学”“科幻”“漫画”“数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率.21. 如图1,已知是的直径,是的切线,交于点 , . (1)、填空:度数是 , 的长为;(2)、求的面积;(3)、如图2, , 垂足为 . 是上一点, . 延长 , 与 , 的延长线分别交于点 , 求的值.22. 为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗.某顾客端午节前在超市购买豆沙粽10个,肉粽12个,共付款136元,已知肉粽单价是豆沙粽的2倍.(1)、求豆沙粽和肉粽的单价;(2)、超市为了促销,购买粽子达20个及以上时实行优惠,下表列出了小欢妈妈、小乐妈妈的购买数量(单位:个)和付款金额(单位:元);
(1)、填空:度数是 , 的长为;(2)、求的面积;(3)、如图2, , 垂足为 . 是上一点, . 延长 , 与 , 的延长线分别交于点 , 求的值.22. 为纪念爱国诗人屈原,人们有了端午节吃粽子的习俗.某顾客端午节前在超市购买豆沙粽10个,肉粽12个,共付款136元,已知肉粽单价是豆沙粽的2倍.(1)、求豆沙粽和肉粽的单价;(2)、超市为了促销,购买粽子达20个及以上时实行优惠,下表列出了小欢妈妈、小乐妈妈的购买数量(单位:个)和付款金额(单位:元);豆沙粽数量
肉粽数量
付款金额
小欢妈妈
20
30
270
小乐妈妈
30
20
230
①根据上表,求豆沙粽和肉粽优惠后的单价;
②为进一步提升粽子的销量,超市将两种粽子打包成A,B两种包装销售,每包都是40个粽子(包装成本忽略不计),每包的销售价格按其中每个粽子优惠后的单价合计.A,B两种包装中分别有m个豆沙粽,m个肉粽,A包装中的豆沙粽数量不超过肉粽的一半.端午节当天统计发现,A,B两种包装的销量分别为包,包,A,B两种包装的销售总额为17280元.求m的值.
23. 如图,在正方形中,E,F分别是边 , 上的点,连接 , , . (1)、若正方形的边长为2,E是的中点.
(1)、若正方形的边长为2,E是的中点.①如图1,当时,求证:;
②如图2,当时,求的长;
(2)、如图3,延长 , 交于点G,当时,求证: .24. 如图,已知 . 点E位于第二象限且在直线上, , , 连接 . (1)、直接判断的形状:是三角形;(2)、求证:;(3)、直线EA交x轴于点 . 将经过B,C两点的抛物线向左平移2个单位,得到抛物线 .
(1)、直接判断的形状:是三角形;(2)、求证:;(3)、直线EA交x轴于点 . 将经过B,C两点的抛物线向左平移2个单位,得到抛物线 .①若直线与抛物线有唯一交点,求t的值;
②若抛物线的顶点P在直线上,求t的值;
③将抛物线再向下平移,个单位,得到抛物线 . 若点D在抛物线上,求点D的坐标.