浙江省杭州市2023年中考数学试卷
试卷更新日期:2023-06-26 类型:中考真卷
一、选择题:本大题共有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
 A、 B、 C、 D、2. ( )A、0 B、2 C、4 D、83. 分解因式:( )A、 B、 C、 D、4. 如图,矩形的对角线相交于点 . 若 , 则( )
A、 B、 C、 D、2. ( )A、0 B、2 C、4 D、83. 分解因式:( )A、 B、 C、 D、4. 如图,矩形的对角线相交于点 . 若 , 则( )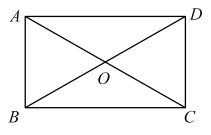 A、 B、 C、 D、5. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、56. 如图,在中,半径互相垂直,点在劣弧上.若 , 则( )
A、 B、 C、 D、5. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、56. 如图,在中,半径互相垂直,点在劣弧上.若 , 则( ) A、 B、 C、 D、7. 已知数轴上的点分别表示数 , 其中 , . 若 , 数在数轴上用点表示,则点在数轴上的位置可能是( )A、
A、 B、 C、 D、7. 已知数轴上的点分别表示数 , 其中 , . 若 , 数在数轴上用点表示,则点在数轴上的位置可能是( )A、 B、
B、 C、
C、 D、
D、 8. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为9. 一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )A、中位数是3,众数是2 B、平均数是3,中位数是2 C、平均数是3,方差是2 D、平均数是3,众数是210. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( )
8. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为9. 一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )A、中位数是3,众数是2 B、平均数是3,中位数是2 C、平均数是3,方差是2 D、平均数是3,众数是210. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题:本题有6个小题,每小题4分,共24分。
-
11. 计算:12. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
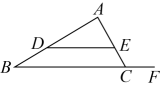 13. 一个仅装有球的不透明布袋里只有6个红球和个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为 , 则 .14. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 .
13. 一个仅装有球的不透明布袋里只有6个红球和个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为 , 则 .14. 如图,六边形是的内接正六边形,设正六边形的面积为 , 的面积为 , 则 . 15. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .
15. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .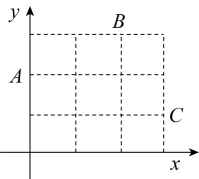 16. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
16. 如图,在中, , 点分别在边 , 上,连接 , 已知点和点关于直线对称.设 , 若 , 则(结果用含的代数式表示).
三、解答题:本大题有7个小题,共66分。解答应写出文字说明、证明过程或演算步骤。
-
17. 设一元二次方程 . 在下面的四组条件中选择其中一组的值,使这个方程有两个不相等的实数根,并解这个方程.
①;②;③;④ .
18. 某校为了了解家长和学生观看安全教育视频的情况,随机抽取本校部分学生作调查,把收集的数据按照A,B,C,D四类(A表示仅学生参与;B表示家长和学生一起参与;C表示仅家长参与;D表示其他)进行统计,得到每一类的学生人数,并把统计结果绘制成如图所示的未完成的条形统计图和扇形统计图. (1)、在这次抽样调查中,共调查了多少名学生?(2)、补全条形统计图.(3)、已知该校共有1000名学生,估计B类的学生人数.19. 如图,平行四边形的对角线相交于点 , 点在对角线上,且 , 连接 , .
(1)、在这次抽样调查中,共调查了多少名学生?(2)、补全条形统计图.(3)、已知该校共有1000名学生,估计B类的学生人数.19. 如图,平行四边形的对角线相交于点 , 点在对角线上,且 , 连接 , . (1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.20. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
(1)、求证:四边形是平行四边形.(2)、若的面积等于2,求的面积.20. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .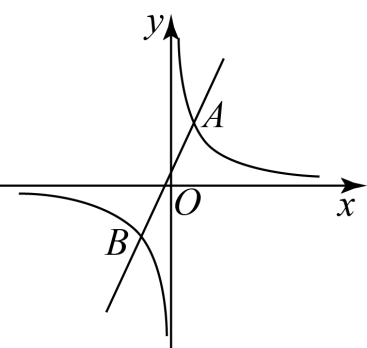 (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.21. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 .
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.21. 在边长为的正方形中,点在边上(不与点 , 重合),射线与射线交于点 . (1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.
(1)、若 , 求的长.(2)、求证: .(3)、以点为圆心,长为半径画弧,交线段于点 . 若 , 求的长.
