【高考真题】2023年北京高考数学卷
试卷更新日期:2023-06-26 类型:高考真卷
一、选择题:本题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 在复平面内,复数对应的点的坐标是 , 则的共轭复数( )A、 B、 C、 D、3. 已知向量满足 , 则( )A、 B、 C、0 D、14. 下列函数中,在区间上单调递增的是( )A、 B、 C、 D、5. 的展开式中的系数为( ).A、 B、 C、40 D、806. 已知抛物线的焦点为 , 点在上.若到直线的距离为5,则( )A、7 B、6 C、5 D、47. 在中, , 则( )A、 B、 C、 D、8. 若 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若 , 且等腰梯形所在的平面、等腰三角形所在的平面与平面的夹角的正切值均为 , 则该五面体的所有棱长之和为( )
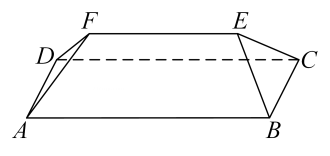 A、 B、 C、 D、10. 已知数列满足 , 则( )A、当时,为递减数列,且存在常数 , 使得恒成立 B、当时,为递增数列,且存在常数 , 使得恒成立 C、当时,为递减数列,且存在常数 , 使得恒成立 D、当时,为递增数列,且存在常数 , 使得恒成立
A、 B、 C、 D、10. 已知数列满足 , 则( )A、当时,为递减数列,且存在常数 , 使得恒成立 B、当时,为递增数列,且存在常数 , 使得恒成立 C、当时,为递减数列,且存在常数 , 使得恒成立 D、当时,为递增数列,且存在常数 , 使得恒成立二、填空题:本题共5小题,每小题5分,共25分.
-
11. 已知函数 , 则 .12. 已知双曲线C的焦点为和 , 离心率为 , 则C的方程为 .13. 已知命题若为第一象限角,且 , 则 . 能说明p为假命题的一组的值为 , .14. 我国度量衡的发展有着悠久的历史,战国时期就已经出现了类似于砝码的、用来测量物体质量的“环权”.已知9枚环权的质量(单位:铢)从小到大构成项数为9的数列 , 该数列的前3项成等差数列,后7项成等比数列,且 , 则;数列所有项的和为 .15. 设 , 函数 , 给出下列四个结论:
①在区间上单调递减;
②当时,存在最大值;
③设 , 则;
④设 . 若存在最小值,则a的取值范围是 .
其中所有正确结论的序号是 .
三、解答题:本题共6小题,共85分.解答应写出文字说明、证明过程或演算步骤.
-
16. 如图,在三棱锥中,平面 , .
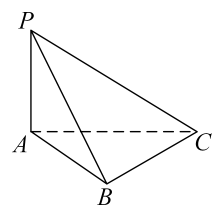 (1)、求证:平面PAB;(2)、求二面角的大小.17. 设函数 .(1)、若 , 求的值.(2)、已知在区间上单调递增, , 再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数存在,求的值.
(1)、求证:平面PAB;(2)、求二面角的大小.17. 设函数 .(1)、若 , 求的值.(2)、已知在区间上单调递增, , 再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数存在,求的值.条件①:;
条件②:;
条件③:在区间上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
18. 为研究某种农产品价格变化的规律,收集得到了该农产品连续40天的价格变化数据,如下表所示.在描述价格变化时,用“+”表示“上涨”,即当天价格比前一天价格高;用“-”表示“下跌”,即当天价格比前一天价格低;用“0”表示“不变”,即当天价格与前一天价格相同.时段
价格变化
第1天到第20天
-
+
+
0
-
-
-
+
+
0
+
0
-
-
+
-
+
0
0
+
第21天到第40天
0
+
+
0
-
-
-
+
+
0
+
0
+
-
-
-
+
0
-
+
用频率估计概率.
(1)、试估计该农产品价格“上涨”的概率;(2)、假设该农产品每天的价格变化是相互独立的.在未来的日子里任取4天,试估计该农产品价格在这4天中2天“上涨”、1天“下跌”、1天“不变”的概率;(3)、假设该农产品每天的价格变化只受前一天价格变化的影响.判断第41天该农产品价格“上涨”“下跌”和“不变”的概率估计值哪个最大.(结论不要求证明)