甘肃省陇南市西和县2022-2023学年七年级下学期4月数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 如图,直线a∥b,∠1=70°,那么∠2的度数是( )
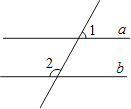 A、130° B、110° C、70° D、80°2. 下列说法中,不正确的是( )A、的立方根是 B、4是16的一个平方根 C、π是无理数 D、的算术平方根是3. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、4. 如图,下列条件:①;②;③;④ , 其中能判断直线与平行的个数是( )
A、130° B、110° C、70° D、80°2. 下列说法中,不正确的是( )A、的立方根是 B、4是16的一个平方根 C、π是无理数 D、的算术平方根是3. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、4. 如图,下列条件:①;②;③;④ , 其中能判断直线与平行的个数是( ) A、1 B、2 C、3 D、45. 如图所示的是一所学校的平面示意图,若用表示教学楼的位置,表示旗杆的位置,则实验楼的位置可表示成( )
A、1 B、2 C、3 D、45. 如图所示的是一所学校的平面示意图,若用表示教学楼的位置,表示旗杆的位置,则实验楼的位置可表示成( ) A、 B、 C、 D、6. 下列命题中,是真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、两条直线被第三条直线所截,同位角的平分线平行 C、垂直于同一条直线的两条直线互相平行 D、对顶角相等,邻补角互补7. 若a和b是两个连续的整数,且满足 , 则的值为( )A、5 B、7 C、9 D、118. 如图所示,共有三个方格块,现将上面的方格块与下面的两个方格块合成一个长方形的整体,应将上面的方格块( )
A、 B、 C、 D、6. 下列命题中,是真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、两条直线被第三条直线所截,同位角的平分线平行 C、垂直于同一条直线的两条直线互相平行 D、对顶角相等,邻补角互补7. 若a和b是两个连续的整数,且满足 , 则的值为( )A、5 B、7 C、9 D、118. 如图所示,共有三个方格块,现将上面的方格块与下面的两个方格块合成一个长方形的整体,应将上面的方格块( ) A、先向右平移1格,再向下平移3格 B、先向右平移1格,再向下平移4格 C、先向右平移2格,再向下平移4格 D、先向右平移2格,再向下平移3格9. 实数在数轴上对应点的位置如图所示,化简的结果是( )
A、先向右平移1格,再向下平移3格 B、先向右平移1格,再向下平移4格 C、先向右平移2格,再向下平移4格 D、先向右平移2格,再向下平移3格9. 实数在数轴上对应点的位置如图所示,化简的结果是( ) A、 B、 C、-b D、b10. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , 那么点为自然数的坐标为 用n表示 .
A、 B、 C、-b D、b10. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , 那么点为自然数的坐标为 用n表示 .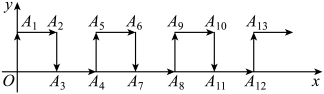 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 比较大小:3(选填“>”,“<”或“=”).12. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为 .
 13. 若 , 则 .14. 在平面直角坐标系中,点到x轴的距离是 .15. 如图,将沿方向平移得到△ , 若的周长为 , 则四边形的周长为 .
13. 若 , 则 .14. 在平面直角坐标系中,点到x轴的距离是 .15. 如图,将沿方向平移得到△ , 若的周长为 , 则四边形的周长为 . 16. 一个小伙伴拿着如图的密码表玩听声音猜单词的游戏,若听到“咚咚一咚咚,咚一咚,咚咚咚一咚”表示的是“”,则听到“咚咚一咚,咚咚咚一咚咚,咚一咚咚咚”时,表示的是 .
16. 一个小伙伴拿着如图的密码表玩听声音猜单词的游戏,若听到“咚咚一咚咚,咚一咚,咚咚咚一咚”表示的是“”,则听到“咚咚一咚,咚咚咚一咚咚,咚一咚咚咚”时,表示的是 .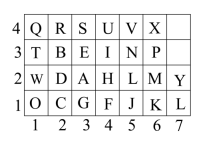 17. 如图,某电脑游戏中,一个小球在同一平面内移动,经过 , , 三点拐弯后移动方向与原来相同,若 , , 则 .
17. 如图,某电脑游戏中,一个小球在同一平面内移动,经过 , , 三点拐弯后移动方向与原来相同,若 , , 则 . 18. 点的坐标为 , 点到的距离为4个单位长度,且轴,则点的坐标为 .
18. 点的坐标为 , 点到的距离为4个单位长度,且轴,则点的坐标为 .三、解答题
-
19. 计算:(1)、;(2)、20. 解方程:(1)、;(2)、 .21. .
解:
. .....第一步
. .....第二步
. .....第三步
(1)、以上解方程的过程中从第步开始出现错误,错误的原因是 .(2)、请写出正确的解方程过程.22. 如图,在平面直角坐标系中,三点的坐标分别为 .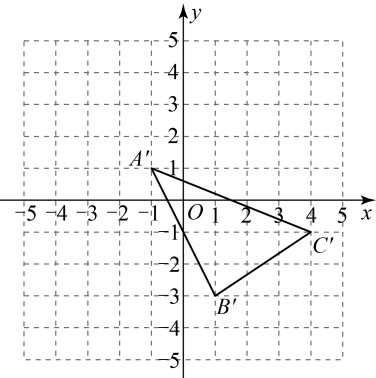 (1)、画出三角形 , 并求其面积;(2)、如图,是由经过怎样的平移得到的?23. 如图, , , DC是的平分线.
(1)、画出三角形 , 并求其面积;(2)、如图,是由经过怎样的平移得到的?23. 如图, , , DC是的平分线. (1)、AB与DE平行吗?请说明理由;(2)、试说明 .24. 填空完成以下证明:
(1)、AB与DE平行吗?请说明理由;(2)、试说明 .24. 填空完成以下证明:已知如图, , , 于点H,求证: .
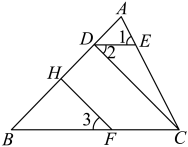
证明:∵(已知),
∴ ▲ .
∵(已知),
∴( ),
∴∠2= ▲ ( ).
∵(已知),
∴∠3= ▲ ( ),
∴( ).
∴ ▲ ( ),
∴ .
25. 大家都知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是 , 将这个数减去其整数部分,差就是小数部分.请解答:(1)、的整数部分为 , 小数部分可以表示为;(2)、已知: , 其中是整数,且 , 请你帮忙确定一下的相反数的值.26. 如图,直线AB,CD被直线EF,MN所截. (1)、若AB∥CD,EF∥MN,∠1=115°,试求∠3和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果填空:如果一个角的两边分别和另一个角的两边平行,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的2倍,求这两个角的度数.27. 问题情境:
(1)、若AB∥CD,EF∥MN,∠1=115°,试求∠3和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果填空:如果一个角的两边分别和另一个角的两边平行,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的2倍,求这两个角的度数.27. 问题情境:在平面直角坐标系中有不重合的两点和 , 小明在学习中发现,若 , 则轴,且线段的长度为;若 , 则轴,且线段的长度为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点 , 之间的折线距离为 . 例如:图1中,点与点之间的折线距离为 .
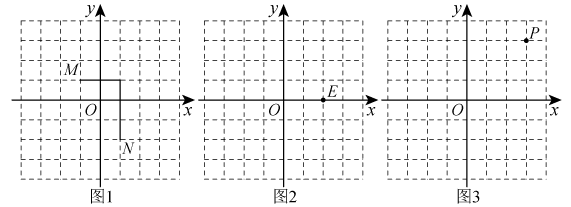
解决下列问题:
(1)、如图2,已知 , 若 , 则;(2)、如图2,已知 , 若 , 则;(3)、如图3,已知 , 点Q在x轴上,且三角形的面积为3,求的值.28.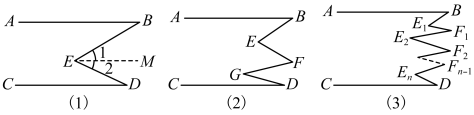 (1)、如图(1), , 探究与的关系:
(1)、如图(1), , 探究与的关系:过点作
∴ ▲
∵ ,
▲
▲
∴ , 即与的关系为: ▲ .
(2)、如图(2), , 类比上述方法,试探究与的关系,并写出推理过程;(3)、如图(3), , 请直接写出你能得到的结论.