甘肃省白银市2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题的因变量是( )A、太阳光强弱 B、水的温度 C、所晒时间 D、热水管2. 如图,两条直线交于点O,若 , 则∠2的度数为( )
 A、40° B、80° C、100° D、140°3. 计算: 的结果是( )A、 B、 C、 D、4. 如图, , 点D到线段的距离指的是下列哪条线段的长度( )
A、40° B、80° C、100° D、140°3. 计算: 的结果是( )A、 B、 C、 D、4. 如图, , 点D到线段的距离指的是下列哪条线段的长度( ) A、 B、 C、 D、5. 若 , 则的值为( )A、 B、 C、 D、6. 如图, , , 则( )
A、 B、 C、 D、5. 若 , 则的值为( )A、 B、 C、 D、6. 如图, , , 则( )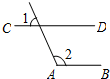 A、 B、 C、 D、7. 计算的值是( )A、1 B、 C、 D、8. 在下列条件中,能判定直线c与d平行的是( )
A、 B、 C、 D、7. 计算的值是( )A、1 B、 C、 D、8. 在下列条件中,能判定直线c与d平行的是( ) A、∠1=∠3 B、∠2=∠5 C、∠2+∠4=180° D、∠4+∠5=180°9. 某人驾车匀速从甲地前往乙地,中途停车休息了一段时间,出发时油箱中有40升油,到乙地后发现油箱中还剩4升油.则油箱中所剩油y(升)与时间t(小时)之间函数图象大致是( )A、
A、∠1=∠3 B、∠2=∠5 C、∠2+∠4=180° D、∠4+∠5=180°9. 某人驾车匀速从甲地前往乙地,中途停车休息了一段时间,出发时油箱中有40升油,到乙地后发现油箱中还剩4升油.则油箱中所剩油y(升)与时间t(小时)之间函数图象大致是( )A、
B、
B、
C、
C、
D、
D、
10. 如图, , 则下列各式中正确的是( )
10. 如图, , 则下列各式中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,不添加辅助线,请写出一个能判定的条件 .
 12. 计算 .13. 如图, , , , 则 .
12. 计算 .13. 如图, , , , 则 . 14. 如图,直线AB与直线CD相交于点O, , 则 .
14. 如图,直线AB与直线CD相交于点O, , 则 . 15. 若 , 则 .16. 旅客乘车按照规定可以携带一定量的行李,若超过规定,则需购买行李票,行李费用y(元)与行李重量x(千克)之间的关系如下表:
15. 若 , 则 .16. 旅客乘车按照规定可以携带一定量的行李,若超过规定,则需购买行李票,行李费用y(元)与行李重量x(千克)之间的关系如下表:行李重量x/千克
…
…
行李费用y/元
…
5
…
根据表中信息,可知携带千克行李所需费用是元.
17. 将一副三角板(含30°、45°、60°、90°角)按如图所示的位置摆放在直尺上,则∠1的度数为°.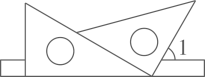 18. 如图,点是延长线上一点,在下列条件中:①;②;③且平分;④ , 能判定的有 . (填序号)
18. 如图,点是延长线上一点,在下列条件中:①;②;③且平分;④ , 能判定的有 . (填序号)
三、解答题
-
19. 已知 , 点C是边上的一点.用尺规作图画出经过点C与平行的直线.
 20. 计算: .21. 如图,AE平分∠BAC,∠CAE=∠CEA..求证: .
20. 计算: .21. 如图,AE平分∠BAC,∠CAE=∠CEA..求证: . 22. 先化简,再求值: , 其中 , .23. 如图,直线 , 相交于点O,平分 , . 若 , 求的度数.
22. 先化简,再求值: , 其中 , .23. 如图,直线 , 相交于点O,平分 , . 若 , 求的度数. 24. 完成下面的求解过程.
24. 完成下面的求解过程.如图, , , , 求的度数.

解:因为(已知),
所以 ▲ ( )
又因为 ,
所以( ),
所以 ▲ ( ),
所以+ ▲ =180°( )
又因为 ,
所以 ▲ .
25. 小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题: (1)、小王在新华书店停留了多长时间?(2)、买到书后,小王从新华书店到商场的骑车速度是多少米/秒?26. 对于任意四个有理数a,b,c,d可以组成两个有理数对与 . 我们规定: , 例如: .(1)、若 , 求常数k的值;(2)、若 , 且 , 求xy的值.27. 根据直尺和三角尺的实物摆放图,解决下列问题.
(1)、小王在新华书店停留了多长时间?(2)、买到书后,小王从新华书店到商场的骑车速度是多少米/秒?26. 对于任意四个有理数a,b,c,d可以组成两个有理数对与 . 我们规定: , 例如: .(1)、若 , 求常数k的值;(2)、若 , 且 , 求xy的值.27. 根据直尺和三角尺的实物摆放图,解决下列问题.


 (1)、如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是;(2)、如图2,图中互余的角有 , 若要使直尺的边缘DE与三角尺的AB边平行,则应满足(填角相等);(3)、如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.28. 问题情境:
(1)、如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是;(2)、如图2,图中互余的角有 , 若要使直尺的边缘DE与三角尺的AB边平行,则应满足(填角相等);(3)、如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.28. 问题情境:在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线 , 连接 , 点是射线上的一个动点(与点不重合), , 分别平分和 , 分别交射线于点 .

探索发现:
“快乐小组”经过探索后发现:
(1)、当时,求证: .(2)、不断改变的度数,与却始终存在某种数量关系,当则度,
当时,则度,(用含的代数式表示)
(3)、 操作探究:“智慧小组”利用量角器量出和的度数后,探究二者之间的数量关系.他们惊奇地发现,当点在射线上运动时,无论点在上的什么位置,与之间的数量关系都保持不变,请写出它们的关系,并说明理由.