甘肃省兰州市教育局第四片区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 有“新材料之王”称号的石墨烯在新能源、电子信息、航天航空、生物医药等领域具有广阔的应用前景.石墨烯中每两个相邻碳原子间的键长为0.000000000142米,数0.000000000142用科学记数法表示是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 在计算( ) ( )时,最佳的方法是( )A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式4. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
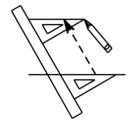 A、两直线平行,同旁内角相等 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、同位角相等,两直线平行5. 如图,已知 , 以点O为圆心,以任意长为半径画弧①,分别交 , 于点 E,F, 再以点 E 为圆心,以长为半径画弧,交弧①于点 D,画射线 . 若 , 则的补角的度数为( )
A、两直线平行,同旁内角相等 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、同位角相等,两直线平行5. 如图,已知 , 以点O为圆心,以任意长为半径画弧①,分别交 , 于点 E,F, 再以点 E 为圆心,以长为半径画弧,交弧①于点 D,画射线 . 若 , 则的补角的度数为( ) A、 B、 C、 D、6. 若 , 则 , 的值分别是( )A、 , B、 , C、 , D、 ,7. 下列说法正确的是( )A、如果两个角相等,那么这两个角是对顶角 B、内错角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角8. 某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
A、 B、 C、 D、6. 若 , 则 , 的值分别是( )A、 , B、 , C、 , D、 ,7. 下列说法正确的是( )A、如果两个角相等,那么这两个角是对顶角 B、内错角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角8. 某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )用电量(千瓦•时)
1
2
3
4
…
应缴电费(元)
0.55
1.10
1.65
2.20
…
A、用电量每增加1千瓦•时,电费增加0.55元 B、若用电量为8千瓦•时,则应缴电费4.4元 C、若应缴电费为2.75元,则用电量为6千瓦•时 D、应缴电费随用电量的增加而增加9. 如图,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠4=∠6;③∠4+∠5=180°;④∠2+∠3=180°.其中能判定a∥b的条件的个数有( ) A、1个 B、2个 C、3个 D、4个10. 已知 则 的大小关系是( )A、 B、 C、 D、11. 一张长方形纸条按如图所示折叠,是折痕,若 , 则:①;②;③;④ . 以上结论正确的有( )
A、1个 B、2个 C、3个 D、4个10. 已知 则 的大小关系是( )A、 B、 C、 D、11. 一张长方形纸条按如图所示折叠,是折痕,若 , 则:①;②;③;④ . 以上结论正确的有( )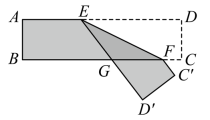 A、①② B、②③④ C、①②③ D、①②③④12. 如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如( , , 即8,16均为“和谐数”),在不超过2023的正整数中,所有的“和谐数”之和为( )A、255054 B、255064 C、250554 D、255024
A、①② B、②③④ C、①②③ D、①②③④12. 如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如( , , 即8,16均为“和谐数”),在不超过2023的正整数中,所有的“和谐数”之和为( )A、255054 B、255064 C、250554 D、255024二、填空题
-
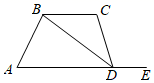
13. 已知 , 则 .14. 如图,在四边形 中,点E在 的延长线上,连接 ,如果添加一个条件,使 ,那么可添加的条件为(写出一个即可).
 15. 计算: .16. 若 , 那么的值为 .17. 如图1,点P从的顶点B出发,沿匀速运动到点A,图2是点P运动时,线段的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则边上的高长为 .
15. 计算: .16. 若 , 那么的值为 .17. 如图1,点P从的顶点B出发,沿匀速运动到点A,图2是点P运动时,线段的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则边上的高长为 .
三、解答题
-
18. 计算题(1)、(2)、(3)、(4)、19. 如图所示是一位病人的体温记录图,看图回答下列问题:
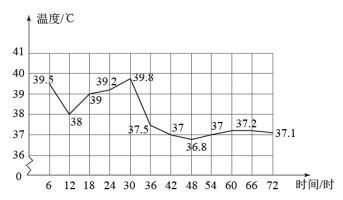 (1)、自变量是 , 因变量是 .(2)、这位病人的最高体温是摄氏度,最低体温是摄氏度.(3)、他在这天12时的体温是摄氏度.20. 请把下列的证明过程补充完整:
(1)、自变量是 , 因变量是 .(2)、这位病人的最高体温是摄氏度,最低体温是摄氏度.(3)、他在这天12时的体温是摄氏度.20. 请把下列的证明过程补充完整:已知:如图, , , 求证: ,
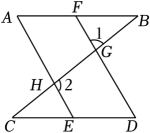
证明:∵与是对顶角,
∴( )
又∵(已知).
∴ ,
∴( )
∴ ( ).
∵(已知),
∴( ),
∴( )
21. 阅读下面这位同学的计算过程,并完成任务.先化简,再求值: , 其中 , .
解:原式第一步
第二步
. 第三步
当 , 时,原式 . 第四步
(1)、第一步运算用到了乘法公式(写出1种即可);(2)、以上步骤第步出现了错误;(3)、请写出正确的解答过程.22. 如图,梯形的上底长是5cm,下底长是13cm当梯形的高由大变小时,梯形的面积也随之发生变化. (1)、求梯形的面积y(cm2)与高x(cm)之间的表达式.(2)、当梯形的高由10cm变化到4cm时,则梯形的面积如何变化?23. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)、求梯形的面积y(cm2)与高x(cm)之间的表达式.(2)、当梯形的高由10cm变化到4cm时,则梯形的面积如何变化?23. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.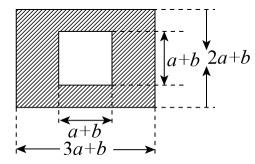 (1)、绿化的面积是多少平方米?(2)、并求出当a=3,b=2时的绿化面积.24. 如图 为直线 上一点, , 平分 , .
(1)、绿化的面积是多少平方米?(2)、并求出当a=3,b=2时的绿化面积.24. 如图 为直线 上一点, , 平分 , .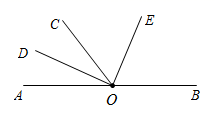 (1)、求 的度数;(2)、试判断 是否平分 ,并说明理由;(3)、 的余角是 .25. 历史上的数学巨人欧拉最先把关于x的多项式用记号来表示.例如: , 当时,多项式的值用来表示.例如时,多项式的值记为 .(1)、已知 , 求值;(2)、已知 , 当 , 求a的值;(3)、已知(为常数),若对于任意有理数k,总有 , 求的值.26. 问题情境
(1)、求 的度数;(2)、试判断 是否平分 ,并说明理由;(3)、 的余角是 .25. 历史上的数学巨人欧拉最先把关于x的多项式用记号来表示.例如: , 当时,多项式的值用来表示.例如时,多项式的值记为 .(1)、已知 , 求值;(2)、已知 , 当 , 求a的值;(3)、已知(为常数),若对于任意有理数k,总有 , 求的值.26. 问题情境我们知道“如果两条平行线被第三条直线所截,所截得的同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化角的作用.
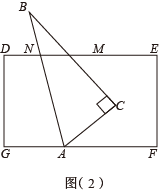
已知三角板ABC中, , , , 长方形DEFG中, .
问题初探
如图(1),若将三角板ABC的顶点A放在长方形的边GF上,BC与DE相交于点M,于点N,则∠EMC的度数是多少呢?
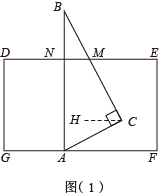
此题有多种解答方法,下面是小军同学的分析过程:
过点C作 , 则 , 这样就将∠CAF转化为∠HCA,∠EMC转化为∠MCH,从而可以求得∠EMC的度数.
(1)、请你直接写出 , ;(2)、 类比再探若将三角板ABC按图(2)所示方式摆放(AB与DE不垂直),请你猜想∠EMC与∠CAF的数量关系,并说明理由;
(3)、 方法迁移请你总结(1)(2)解决问题的思路,在图(2)中探究∠BAG与∠BMD的数量关系,并直接写出结果.