重庆市潼南区六校2022-2023学年七年级下学期数学期中考试试卷

试卷更新日期：2023-06-26 类型：期中考试

进入出卷网下载

一、单选题

1. 冰墩墩是深受大家喜爱的北京冬奥会吉祥物，它寓意创造非凡、探索未来．下列图形中可看作是由左侧“冰墩墩”图形平移后得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数 $3.141$ ， $\sqrt{8}$ ， $π$ ， $- \frac{3}{2}$ ， $0 . \dot{5}$ ， $0.1010010001 \dots ($ 每相邻两个 $1$ 之间依次多一个 $0)$ 中，无理数有个（）．

A、 $5$ B、 $4$ C、 $3$ D、 $2$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{9}$ ＝±3 B、 $\sqrt[3]{- 8}$ ＝﹣2 C、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3 D、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$

查看试题解析
4. 图中，直线 $a$ ， $b$ 相交， $∠ 1$ ： $∠ 2 = 2$ ： $7$ ，则 $∠ 3$ 的度数是（）

A、 $20 °$ B、 $60 °$ C、 $45 °$ D、 $40 °$

查看试题解析
5. 已知 $a < b < 0$ ，则点 $A (a - b ， a b)$ 在（）．

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 估算 $\sqrt{11} - 2$ 的值在（）

A、 $1$ 和 $2$ 之间 B、 $2$ 和 $3$ 之间 C、 $3$ 和 $4$ 之间 D、 $4$ 和 $5$ 之间

查看试题解析
7. 如图，直线 $A B ∥ C D$ ，一块含有 $30 °$ 角的直角三角尺的顶点E位于直线 $C D$ 上， $E G$ 平分 $∠ C E F$ ，则 $∠ 1$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $80 °$

查看试题解析
8. 我国古典数学文献 $《$ 增删算法统宗 $\cdot$ 六均输 $》$ 中这样一道题：甲、乙两人一同放牧，两人暗地里数羊，如果乙给甲 $9$ 只羊，则甲的羊数为乙的两倍；如果甲给乙 $9$ 只羊，则两人的羊数相同，设甲有羊 $x$ 只，乙有羊 $y$ 只，根据题意，可列方程组为（　　　）

A、 ${\begin{array}{l} x - 9 = 2 (y + 9) \\ x - 9 = y + 9 \end{array}$ B、 ${\begin{array}{l} 2 (x + 9) = y - 9 \\ x - 9 = y + 9 \end{array}$ C、 ${\begin{array}{l} x + 9 = 2 (y - 9) \\ x - 9 = y + 9 \end{array}$ D、 ${\begin{array}{l} x - 9 = 2 (y + 9) \\ x + 9 = y - 9 \end{array}$

查看试题解析
9. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动一个单位，得到点A₁（0，1），A₂（1，1），A₃（1，0），A₄（2，0），…，那么点A₄n₊₁（n是自然数）的坐标为（）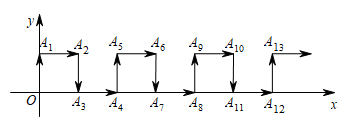

A、（1，2n） B、（2n，1） C、（n，1） D、（2n-1，1）

查看试题解析
10. 下列说法不正确的个数有（）
①垂线段最短；②同旁内角互补；③平行于同一条直线的两条直线互相平行；④无限小数都是无理数；⑤如果 $m$ 是任意实数，则点 $P (m + 1 ， m - 3)$ 一定不在第二象限．

A、 $5$ 个 B、 $4$ 个 C、 $3$ 个 D、 $2$ 个

查看试题解析

二、填空题

11. 64的平方根是．

查看试题解析
12. 把命题“邻补角互补”改写成“如果…，那么…”的形式．

查看试题解析
13. 若 $(m - 1) x y + 9 x + 3 y^{n - 2} = 7$ 是关于 $x$ ， $y$ 的二元一次方程，则 $m =$ ， $n =$ ．

查看试题解析
14. 点 $P (m + 2 ， m - 1)$ 在y轴上，则点P的坐标是．

查看试题解析
15. 把实数 $2$ ， $\sqrt{5}$ ， $\sqrt[3]{7}$ 用“ $<$ ”符号连接起来为．

查看试题解析
16. 线段 $A B = 6$ ， $A B ∥$ $y$ 轴，若点 $A$ 的坐标为 $(- 1 ， 3)$ ，则点 $B$ 的坐标为．

查看试题解析
17. 已知 $a$ ， $b$ ， $c$ 都是实数，且满足 $(2 - a)^{2} + \sqrt{a^{2} + b + c} + | c + 8 | = 0$ ，且 $a x^{2} + b x + c = 0$ ，则代数式 $3 x^{2} + 6 x + 2011$ 的值是．

查看试题解析
18. 对于一个三位正整数 $Q = \bar{a b c}$ ，若各个数位上的数字都不为 $0$ ，且百位数字与个位数字之和恰好等于十位数字的两倍，则称这个三位正整数 $Q$ 叫“中项两倍数” $.$ 把“中项两倍数” $Q$ 的各个数字之和被 $3$ 整除的商记为 $F (Q) .$ 其中，能被 $21$ 整除，且 $\sqrt{F (Q)}$ 为有理数的所有“中项两倍数” $Q$ 的值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{16} + \sqrt[3]{- 8} - \sqrt{{(- 2)}^{2}}$ ；

(2)、 $| 1 - \sqrt{2} | - (\sqrt{3} - \sqrt{2}) - | \sqrt{3} - 2 | + (- 1)^{2023}$ ．

查看试题解析
20. 解下列方程组：

(1)、 ${\begin{array}{l} m - 2 n = 4 \\ 5 m - 3 n = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + y = 5 \\ \frac{x + 1}{2} - \frac{y - 1}{3} = \frac{2}{3} \end{array}$ ．

查看试题解析
21. 已知：如图， $∠ B + ∠ B D G = 180 °$ ，点 $E$ 为线段 $B C$ （除除 $B$ 、 $C$ 外）的任一点．

(1)、过点 $E$ 作 $E F ∥ C D$ 交 $A B$ 于点 $F$ ；

(2)、试说明 $∠ B E F = ∠ C D G .$ 将下面的证明过程补充完整，括号内写上相应理由或依据：
证明：∵EF∥CD（已知），

$∴ ∠ B E F =$        ▲  （        ）

又 $∵ ∠ B + ∠ B D G = 180 °$ （已知），

$∴$ $B C ∥$        ▲  （        ）

$∴ ∠ C D G =$         ▲  （        ）

$∴ ∠ C D G = ∠ B E F$ （        ）

查看试题解析
22. 已知在平面直角坐标系中有三点 $A (1 ， - 1)$ ， $B (4 ， - 2)$ ， $C (2 ， - 5)$ ，请回答如下问题：

(1)、在坐标系内平移 $△ A B C$ ，使点 $A$ 的对应点 $A'$ 的坐标为 $(- 4 ， 4)$ ，画出 $△ A' B' C'$ ，并直接写出点 $B'$ 、 $C'$ 的坐标；

(2)、若 $M (m ， n)$ 是 $△ A B C$ 内部任意一点，请直接写出这点在 $△ A' B' C'$ 内部对应点 $M'$ 的坐标：；

(3)、求出 $△ A B C$ 的面积．

查看试题解析
23. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x - 3 y = - 10 \\ a x + b y = 14 \end{array}$ 和方程组 ${\begin{array}{l} 3 x + 2 y = 11 \\ a y - b x = 5 \end{array}$ 的解相同．

(1)、这两个方程组的解；

(2)、求 $(2 a + b)$ 的立方根．

查看试题解析
24. 一艘轮船在甲、乙两地之间匀速航行，从甲地到乙地顺流航行用 $6$ 小时，从乙地到甲地逆流航行用 $10$ 小时 $.$ 已知当时平均水流速度为每小时 $4$ 千米．

(1)、求该轮船在静水中的速度及甲乙两地的距离；

(2)、若在甲、乙两地之间的丙地新建一个码头，使该轮船从甲地匀速航行到丙地和从乙地匀速航行到丙地所用的航行时间相同 $($ 其中轮船的静水速度不变 $)$ ，问甲、丙两地相距多少千米？

查看试题解析
25. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ，且 $∠ 3 = ∠ C$ ．

(1)、求证：判断 $E F$ 与 $B C$ 的位置关系，并说明理由；

(2)、若 $B E$ 平分 $∠ A B C$ ，且 $∠ 2 = 100 °$ ， $∠ 3 = 55 °$ ，求 $∠ A B C$ 的度数．

查看试题解析
26. 如图 $(a)$ ，直线 $A C ∥ B D$ ，直线 $A C$ 、 $B D$ 及直线 $A B$ 把平面分成①、②、③、④、⑤、⑥六个部分，点 $P$ 是其中的一个动点，连接 $P A$ 、 $P B$ ，观察 $∠ A P B$ 、 $∠ P A C$ 、 $∠ P B D$ 三个角 $.$ 规定：直线 $A C$ 、 $B D$ 、 $A B$ 上的各点不属于①、②、③、④、⑤、⑥六个部分中的任何一个部分．

(1)、当动点 $P$ 落在第①部分时 $($ 图 $(b))$ ，可得： $∠ A P B = ∠ P A C + ∠ P B D$ ，请说明理由．

(2)、当动点 $P$ 落在第②部分时 $($ 图 $(c))$ ， $∠ A P B$ 、 $∠ P A C$ 、 $∠ P B D$ 之间的关系是怎样的？请直接写出 $∠ A P B$ 、 $∠ P A C$ 、 $∠ P B D$ 之间满足的关系式，并说明理由．

(3)、当动点 $P$ 在第③部分时， $∠ A P B$ 、 $∠ P A C$ 、 $∠ P B D$ 之间的关系是怎样的？请直接写出相应的结论．

查看试题解析