贵州省河口乡梅江普通中学2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 下列选项中,和是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 根据下列表述,能确定位置的是( )A、某电影院2排 B、大桥南路 C、北偏东 D、东经 , 北纬3. 如图,在直线l外一点P与直线上各点的连线中,PA=5,PO=4,PB=4.3,OC=3,则点P到直线l的距离为( )
2. 根据下列表述,能确定位置的是( )A、某电影院2排 B、大桥南路 C、北偏东 D、东经 , 北纬3. 如图,在直线l外一点P与直线上各点的连线中,PA=5,PO=4,PB=4.3,OC=3,则点P到直线l的距离为( ) A、3 B、4 C、4.3 D、54. 要说明命题“若 , 则”是假命题,可以举的一个反例是( )A、 B、 C、 D、5. 如图,下列能判定的条件有( )
A、3 B、4 C、4.3 D、54. 要说明命题“若 , 则”是假命题,可以举的一个反例是( )A、 B、 C、 D、5. 如图,下列能判定的条件有( )①;②;③;④ .
 A、1个 B、2个 C、3个 D、4个6. 已知x、y是二元一次方程组的解,那么的值是( )A、 B、 C、 D、7. 如图,直线、被直线所截,已知 , , 则的度数为( )
A、1个 B、2个 C、3个 D、4个6. 已知x、y是二元一次方程组的解,那么的值是( )A、 B、 C、 D、7. 如图,直线、被直线所截,已知 , , 则的度数为( ) A、 B、 C、 D、8. 实数m,n在数轴上对应点的位置如图所示,则下列判断错误的是( )
A、 B、 C、 D、8. 实数m,n在数轴上对应点的位置如图所示,则下列判断错误的是( ) A、 B、 C、 D、9. 如图,直角三角形沿斜边的方向平移到直角三角形的位置,则平移的距离是( )
A、 B、 C、 D、9. 如图,直角三角形沿斜边的方向平移到直角三角形的位置,则平移的距离是( )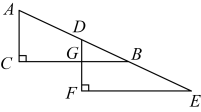 A、线段 B、线段的长度 C、线段的长度 D、线段的长度10. 已知点 , 点 , 且直线轴,则m的值为( )A、 B、1 C、 D、311. 按下图所示程序框图计算,若输入的值为 , 则输出结果为( )
A、线段 B、线段的长度 C、线段的长度 D、线段的长度10. 已知点 , 点 , 且直线轴,则m的值为( )A、 B、1 C、 D、311. 按下图所示程序框图计算,若输入的值为 , 则输出结果为( ) A、 B、 C、4 D、12. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A、 B、 C、4 D、12. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( ) A、57° B、58° C、59° D、60°
A、57° B、58° C、59° D、60°二、填空题
-
13. 如图,直线a,b被直线c所截,则∠2的内错角是 .
 14. 如图所示, 于点F,则 .
14. 如图所示, 于点F,则 .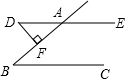 15. 如图,有一个体积为的魔方,则魔方的表面积为.
15. 如图,有一个体积为的魔方,则魔方的表面积为. 16. 如图,长方形的各边分别平行于x轴或y轴,甲,乙两物体分别由点同时出发,沿长方形的边作环绕运动,物体甲按逆时针方向以1个单位/秒的速度匀速运动,物体乙按顺时针方向以2个单位/秒的速度匀速运动,则两物体运动后第2023次相遇的地点坐标是 .
16. 如图,长方形的各边分别平行于x轴或y轴,甲,乙两物体分别由点同时出发,沿长方形的边作环绕运动,物体甲按逆时针方向以1个单位/秒的速度匀速运动,物体乙按顺时针方向以2个单位/秒的速度匀速运动,则两物体运动后第2023次相遇的地点坐标是 .
三、解答题
-
17. 计算:(1)、:(2)、 .18. 解方程组:(1)、;(2)、 .19. 如图,平面直角坐标系中,的顶点都在正方形网格的格点上,其中A点坐标为 .
 (1)、请直接写出点B、C的坐标;(2)、若把向上平移3个单位长度,再向右平移3个单位长度得到 , 画出;(3)、求的面积.20. 如图,已知ABCD,射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: .
(1)、请直接写出点B、C的坐标;(2)、若把向上平移3个单位长度,再向右平移3个单位长度得到 , 画出;(3)、求的面积.20. 如图,已知ABCD,射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: .
证明:∵ABCD(已知)
∴ ▲ (两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴BC ▲ (同旁内角互补,两直线平行)
∴ ▲ ( )
∵ ▲ (对顶角相等.)
∴(等量代换)
21. 已知点P(8-2m,m+1).(1)、若点P在y轴上,求m的值.(2)、若点P在第一象限,且点P到x轴的距离是到y轴距离的2倍,求P点的坐标.22. 如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变. (1)、请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?(2)、若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.23. 已知方程是关于x,y的二元一次方程.(1)、求m,n的值:(2)、求时,y的值.24. 我们用表示不大于的最大整数,的值称为数的小数部分,如 , 的小数部分为 .(1)、 , , 的小数部分 .(2)、已知: , 其中是整数;且 , 求的相反数.25. 如图,在直角中, , 将沿AB方向平移至 , cm,cm.
(1)、请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?(2)、若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.23. 已知方程是关于x,y的二元一次方程.(1)、求m,n的值:(2)、求时,y的值.24. 我们用表示不大于的最大整数,的值称为数的小数部分,如 , 的小数部分为 .(1)、 , , 的小数部分 .(2)、已知: , 其中是整数;且 , 求的相反数.25. 如图,在直角中, , 将沿AB方向平移至 , cm,cm. (1)、AC和DF的数量关系为 , 位置关系为;(2)、°;(3)、求沿AB方向平移的距离;(4)、若cm,求四边形AEFC的周长.26. 据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙,华罗庚讲述了计算过程:
(1)、AC和DF的数量关系为 , 位置关系为;(2)、°;(3)、求沿AB方向平移的距离;(4)、若cm,求四边形AEFC的周长.26. 据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙,华罗庚讲述了计算过程:第一步:因为 , , , 所以 .
第二步:因为59319的个位上的数是9,只有个位数字是9的数的立方的个位数字是9,所以的个位数字是9.
第三步:如果划去59319后面的三位319得到数59,而 , , 所以 ,
所以 , 即的十位数字是3.
所以 .
请根据上述材料解答下列问题:
(1)、用上述方法确定4913的立方根的个位数字是 .(2)、用上述方法确定50653的立方根是 .(3)、求的值,要求写出计算过程.