河北省石家庄地区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 将75500000用科学记数法表示为( )A、 B、 C、 D、2. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等3. 计算的结果是( )A、 B、 C、 D、4. 用加减消元法解二元一次方程组时,下列方法中无法消元的是( )A、①×2-② B、②×(-3)-① C、①×(-2)+② D、①-②×35. 如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等3. 计算的结果是( )A、 B、 C、 D、4. 用加减消元法解二元一次方程组时,下列方法中无法消元的是( )A、①×2-② B、②×(-3)-① C、①×(-2)+② D、①-②×35. 如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )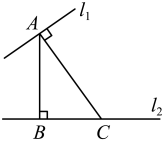 A、点B到直线l1的距离等于4 B、点A到直线l2的距离等于5 C、点B到直线l1的距离等于5 D、点C到直线l1的距离等于56. 若 , 则p、q的值是( )A、2, B、 , C、 , 8 D、2,87. 小张利用如图①所示的长为a、宽为b的长方形卡片4张,拼成了如图②所示的图形,则根据图②的面积关系能验证的恒等式为( )
A、点B到直线l1的距离等于4 B、点A到直线l2的距离等于5 C、点B到直线l1的距离等于5 D、点C到直线l1的距离等于56. 若 , 则p、q的值是( )A、2, B、 , C、 , 8 D、2,87. 小张利用如图①所示的长为a、宽为b的长方形卡片4张,拼成了如图②所示的图形,则根据图②的面积关系能验证的恒等式为( )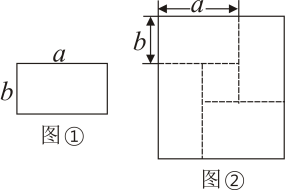 A、 B、 C、 D、8. 若 , , 则等于( )A、 B、6 C、21 D、209. 如图,下列推理正确的是( )
A、 B、 C、 D、8. 若 , , 则等于( )A、 B、6 C、21 D、209. 如图,下列推理正确的是( )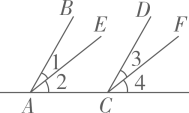 A、因为∠1=∠3,所以AB∥CD B、因为∠1=∠3,所以AE∥CF C、因为∠2=∠4,所以AB∥CD D、因为∠4=∠2,所以AE∥CF10. 如图, , 将直角沿着射线方向平移10个单位长度,得 , 已知 , , 则阴影部分的面积为( )
A、因为∠1=∠3,所以AB∥CD B、因为∠1=∠3,所以AE∥CF C、因为∠2=∠4,所以AB∥CD D、因为∠4=∠2,所以AE∥CF10. 如图, , 将直角沿着射线方向平移10个单位长度,得 , 已知 , , 则阴影部分的面积为( )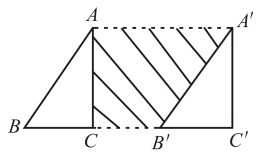 A、40 B、60 C、20 D、8011. 如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A、40 B、60 C、20 D、8011. 如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
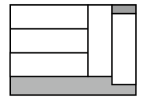 A、35 B、45 C、55 D、6512. 已知,直线m∥n,将含30°的直角三角板按照如图位置放置,∠1=25°,则∠2等于( )
A、35 B、45 C、55 D、6512. 已知,直线m∥n,将含30°的直角三角板按照如图位置放置,∠1=25°,则∠2等于( )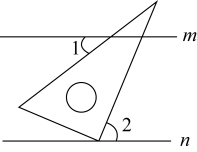 A、35° B、45° C、55° D、65°
A、35° B、45° C、55° D、65°二、填空题
-
13. 计算: .14. 下列各式中:①(-a2)3;②(-a3)2;③(-a)5(-a);④(-a2)(-a)4 . 其中计算结果等于-a6的是 . (只填写序号)15. 配方法是数学中非常重要的一种思想方法,它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.这种方法常被用到代数式的变形中,并结合非负数的意义来解决问题.定义:若一个整数能表示成(a,b为整数)的形式,则称这个数为“完美数”.例如,5是“完美数”,理由:因为 , 所以5是“完美数”.解决问题:已知40是“完美数”,请将它写成(a,b为整数)的形式: .16. 若 , , 则ab= .17. 如图所示,过点P画直线a的平行线b的作法的依据是 .
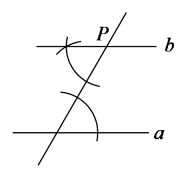 18. 如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是
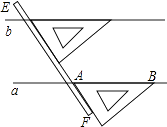
18. 如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是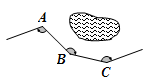 19. 新定义:如果a,b都是非零整数,且 , 那么就称a是“4倍数”.
19. 新定义:如果a,b都是非零整数,且 , 那么就称a是“4倍数”.验证:嘉嘉说:是“4倍数”,琪琪说:也是“4倍数”,判断说得对(填“嘉嘉”、“琪琪”或“嘉嘉、琪琪”).
20. 已知 , 则的个位数字是 .三、解答题
-
21. 有一种长度单位叫纳米 , , 现用边长为1纳米的小正方体堆垒成边长为1cm的正方体要用多少个边长为1纳米的小正方体?22. 化简后求值 , 其中 , .23. 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积,并求当时代数式的值是多少.