河北省张家口市宣化区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 如图,将一张长方形纸对折两次,则这两条折痕的位置关系是( )
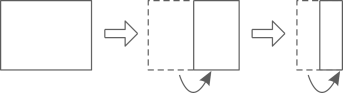 A、平行 B、垂直 C、平行或垂直 D、无法确定2. 下列方程中,是二元一次方程的是( )A、xy=2 B、3x=4y C、x+ =2 D、x2+2y=43. 下列运算正确的是( )A、 B、 C、 D、4. 下列命题中,为真命题的是( )A、若 , 则 B、若 , 则 C、同位角相等 D、对顶角相等5. 下列各式中一定正确的是 ( )A、(2x-3)0=1 B、0=0 C、(2-1)0=1 D、(m2+1)0=16. 如图,点在直线上, , 若 , 则的大小为( )
A、平行 B、垂直 C、平行或垂直 D、无法确定2. 下列方程中,是二元一次方程的是( )A、xy=2 B、3x=4y C、x+ =2 D、x2+2y=43. 下列运算正确的是( )A、 B、 C、 D、4. 下列命题中,为真命题的是( )A、若 , 则 B、若 , 则 C、同位角相等 D、对顶角相等5. 下列各式中一定正确的是 ( )A、(2x-3)0=1 B、0=0 C、(2-1)0=1 D、(m2+1)0=16. 如图,点在直线上, , 若 , 则的大小为( )
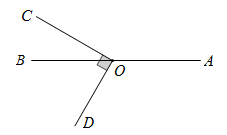 A、30° B、40° C、50° D、60°7. 若方程组用代入法消去 , 所得关于的一元一次方程为( )A、 B、 C、 D、8. 如图, , , 点D是射线上的一个动点,则线段的长度不可能是( )
A、30° B、40° C、50° D、60°7. 若方程组用代入法消去 , 所得关于的一元一次方程为( )A、 B、 C、 D、8. 如图, , , 点D是射线上的一个动点,则线段的长度不可能是( ) A、5.5 B、6 C、8 D、159. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中 , 都与地面l平行, , . 当为( )度时,与平行.
A、5.5 B、6 C、8 D、159. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中 , 都与地面l平行, , . 当为( )度时,与平行.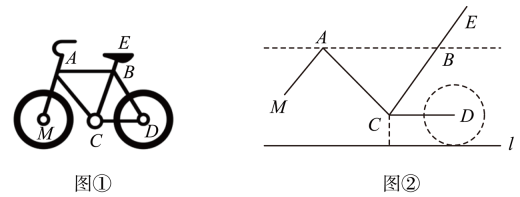 A、16 B、60 C、66 D、11410. 若与可以合并成一项,则mn的值是( )A、2 B、0 C、-1 D、111. 已知直线mn,如图,下列哪条线段的长可以表示直线与之间的距离( )
A、16 B、60 C、66 D、11410. 若与可以合并成一项,则mn的值是( )A、2 B、0 C、-1 D、111. 已知直线mn,如图,下列哪条线段的长可以表示直线与之间的距离( )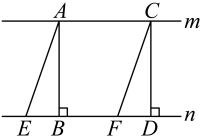 A、只有 B、只有 C、和均可 D、和均可12. 如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A、只有 B、只有 C、和均可 D、和均可12. 如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( ) A、 B、 C、 D、13. 若关于x,y的方程组的解适合方程 , 则m的值为( )A、 B、1 C、2 D、314. 将一张边沿互相平行的纸条如图折叠后,若边 ,则翻折角 与 一定满足的关系是( )
A、 B、 C、 D、13. 若关于x,y的方程组的解适合方程 , 则m的值为( )A、 B、1 C、2 D、314. 将一张边沿互相平行的纸条如图折叠后,若边 ,则翻折角 与 一定满足的关系是( )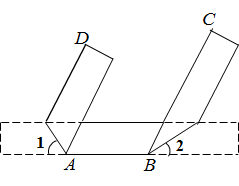 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
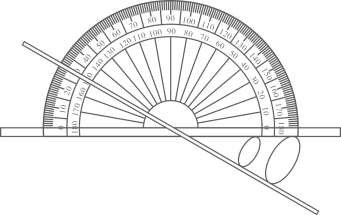
15. 如图所示方式摆放纸杯测量角的基本原理是 .
 16. 计算: .17. 如图表示钉在一起的木条a,b,c.若测得 , 要使木条 , 木条a至少要旋转°.
16. 计算: .17. 如图表示钉在一起的木条a,b,c.若测得 , 要使木条 , 木条a至少要旋转°.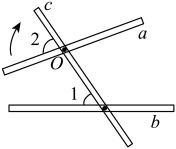 18. 已知关于 , 的方程组 , 其中 . 下列结论:①当时, , 的值互为相反数;②是方程组的解;③当时,方程组的解也是方程的解.其中正确的是 .19. 今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是次.20. 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第秒时,边CD恰好与边AB平行.
18. 已知关于 , 的方程组 , 其中 . 下列结论:①当时, , 的值互为相反数;②是方程组的解;③当时,方程组的解也是方程的解.其中正确的是 .19. 今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是次.20. 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第秒时,边CD恰好与边AB平行.
三、解答题
-
21. 已知关于x,y的二元一次方程组.(1)、当方程组的解为时,求a的值.(2)、当a=﹣2时,求方程组的解.(3)、小冉同学模仿第(1)问,提出一个新解法:将代入方程x+2y=a中,即可求出a的值.小冉提出的解法对吗?若对,请完成解答;若不对,请说明理由.22.(1)、已知 , , 求;(2)、已知 , 求的值.23. 数学课上,陈老师说:“同学们,如果 的两边与 的两边分别平行,你能根据这个条件画出图形并探讨一下 与 的数量关系吗?”
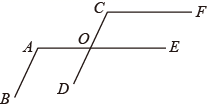 (1)、甲同学很快画出了如图所示的图形,并根据 , 的条件,得出了 的结论,请你帮他写出说理过程.(2)、甲同学由此告诉陈老师:“我的结论是:如果两个角的两边分别平行,那么这两个角相等.”你同意甲同学的结论吗? . (填“同意”或“不同意”).如果不同意,请写出你的结论: .24. 阅读探索.
(1)、甲同学很快画出了如图所示的图形,并根据 , 的条件,得出了 的结论,请你帮他写出说理过程.(2)、甲同学由此告诉陈老师:“我的结论是:如果两个角的两边分别平行,那么这两个角相等.”你同意甲同学的结论吗? . (填“同意”或“不同意”).如果不同意,请写出你的结论: .24. 阅读探索.知识累积:解方程组 ,
解:设 , , 原方程组可变为
解方程组,得: , 即 , 解得 . 此种解方程组的方法叫换元法 .
(1)、举一反三:运用上述方法解下列方程组:;(2)、能力运用:已知关于 , 的方程组的解为 , 则关于 , 的方程组的解是;(3)、拓展提高:若方程组的解是 , 则方程组的解是 .25. 糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个? 26. 某学习小组发现一个结论:已知直线a//b,若直线c//a,则c//b,他们发现这个结论运用很广,请你利用这个结论解决以下问题:
26. 某学习小组发现一个结论:已知直线a//b,若直线c//a,则c//b,他们发现这个结论运用很广,请你利用这个结论解决以下问题:已知直线AB//CD,点E在AB,CD之间,点P,Q分别在直线AB,CD上,连接PE,EQ.
 (1)、如图1,作EH//AB,运用上述结论,探究∠PEQ与∠APE+∠CQE间的数量关系,并说明理由;(2)、如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;(3)、如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,直接写出∠PFQ的度数.
(1)、如图1,作EH//AB,运用上述结论,探究∠PEQ与∠APE+∠CQE间的数量关系,并说明理由;(2)、如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;(3)、如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,直接写出∠PFQ的度数.