湖南省永州市道县2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 下列方程组中,表示二元一次方程组的是( )A、 B、 C、 D、2. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 下列运算一定正确的是( ).A、 B、 C、 D、4. 若是方程组的解,则的值为( )A、16 B、-1 C、-16 D、15. 若长和宽分别是的长方形的周长为10,面积为4,则的值为( )A、14 B、16 C、20 D、406. 计算的值是( )A、 B、 C、 D、27. 如果y2-ay+81是一个完全平方式,那么a的值是( )A、18 B、-18 C、±18 D、以上选项都错8. 下列各式中不能用公式法分解因式的是A、x2-6x+9 B、-x2+y2 C、x2+2x+4 D、-x2+2xy-y29. 如图, , , 点B,O,D在同一条直线上,∠2=( )
 A、 B、 C、 D、10. 如图,根据阴影部分面积和图形的面积关系可以得到的数学公式是( )
A、 B、 C、 D、10. 如图,根据阴影部分面积和图形的面积关系可以得到的数学公式是( )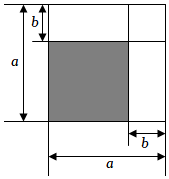 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 解方程组时,一学生把c看错得 , 已知方程组的正确解是 , 则abc值为 .12. 计算: .13. 已知|x-y+2|+(x+y-2)2=0,则x2-y2的值为 .14. 计算: .15. 如图,在中, , 将沿方向平移的长度得到 , 已知.则图中阴影部分的面积 .
 16. 对于x,y,定义新运算x⊗y=ax+by-3(其中a,b是常数),等式的右边是通常的加法与乘法运算,已知1⊗2=9,(-3)⊗3=6,则2⊗(-7)= .17. 若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是 .18. 已知关于x,y的二元一次方程组有下列说法:①当x与y相等时,解得;②当x与y互为相反数时,解得;③若 , 则;④无论k为何值,x与y的值一定满足关系式 , 其中正确的序号是 .
16. 对于x,y,定义新运算x⊗y=ax+by-3(其中a,b是常数),等式的右边是通常的加法与乘法运算,已知1⊗2=9,(-3)⊗3=6,则2⊗(-7)= .17. 若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是 .18. 已知关于x,y的二元一次方程组有下列说法:①当x与y相等时,解得;②当x与y互为相反数时,解得;③若 , 则;④无论k为何值,x与y的值一定满足关系式 , 其中正确的序号是 .三、解答题
-
19. 解方程组:(1)、(2)、20. 利用因式分解计算:(1)、(2)、21. 先化简,再求值: , 其中22. 数学活动课上,小云和小辉在讨论老师出示的一道二元一次方程组的问题:
已知关于 , 的二元一次方程组的解满足③,求的值.
 (1)、按照小云的方法,的值为 , 的值为;(2)、请按照小辉的思路求出的值.23. 去年年底,重庆疫情形势严峻,除了医务人员和志愿者们主动请缨走向抗疫前线,众多企业也纷纷伸出援助之手.某公司租用A、B两种货车向重庆运送抗疫物资,已知用2辆A型车和3辆B型车载满货物一次可运物资吨;用1辆A型车和4辆B型车载满货物一次可运物资吨.(1)、求1辆A型车和1辆B型车都装满货物一次可分别运送多少吨物资?(2)、现有吨抗疫物资需要运往重庆,该公司计划同时租用A型车和B型车(两种型号车均要租用),一次运完,且恰好每辆车都装满货物.若A型车每辆需租金元/次,B型车每辆需租金元/次.那么该公司有哪几种租车方案,并且哪种方案租车费用最少.24. 【阅读理解】
(1)、按照小云的方法,的值为 , 的值为;(2)、请按照小辉的思路求出的值.23. 去年年底,重庆疫情形势严峻,除了医务人员和志愿者们主动请缨走向抗疫前线,众多企业也纷纷伸出援助之手.某公司租用A、B两种货车向重庆运送抗疫物资,已知用2辆A型车和3辆B型车载满货物一次可运物资吨;用1辆A型车和4辆B型车载满货物一次可运物资吨.(1)、求1辆A型车和1辆B型车都装满货物一次可分别运送多少吨物资?(2)、现有吨抗疫物资需要运往重庆,该公司计划同时租用A型车和B型车(两种型号车均要租用),一次运完,且恰好每辆车都装满货物.若A型车每辆需租金元/次,B型车每辆需租金元/次.那么该公司有哪几种租车方案,并且哪种方案租车费用最少.24. 【阅读理解】完全平方公式:适当的变形,可以解决很多的数学问题.
例:若 , 求的值.
解:∵ , ∴
∴
∴
根据上面的解题思路与方法,解决下列问题:
(1)、若 , 则;(2)、 类比应用:若 , 求的值;
(3)、思维拓展:如图,点是线段上的一点,以为边向两边作正方形,若 , 两正方形的面积和 , 求图中阴影部分面积. 25. 如图1,点为直线上一点,过点作射线 , 使 . 将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
25. 如图1,点为直线上一点,过点作射线 , 使 . 将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.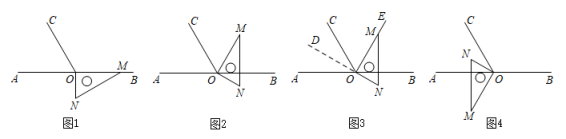 (1)、将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分 , 求的度数;(2)、在图3中,延长线段得到射线 , 判断是否平分 , 请说明理由.(3)、将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角 , 则的值为 . (直接写出答案)
(1)、将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分 , 求的度数;(2)、在图3中,延长线段得到射线 , 判断是否平分 , 请说明理由.(3)、将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角 , 则的值为 . (直接写出答案)