重庆市江北区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-26 类型:期中考试
一、单选题
-
1. 在下列各数0,0.2, , , 6.1010010001…(1之间逐次增加一个0), , 中,无理数的个数是( )A、1 B、2 C、3 D、42. 如图,下列说法错误的是( ).
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
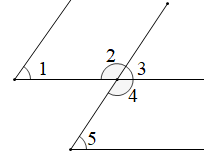 A、①② B、②③ C、②④ D、③④3. 第二象限内的点P(x,y)满足|x|=9,y2=4,则点P 的坐标是( )A、 B、 C、 D、4. 如图,下列能判断AB∥CD的条件有( )
A、①② B、②③ C、②④ D、③④3. 第二象限内的点P(x,y)满足|x|=9,y2=4,则点P 的坐标是( )A、 B、 C、 D、4. 如图,下列能判断AB∥CD的条件有( )①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5.
 A、①② B、②③ C、①③ D、②④5. 以为解的二元一次方程组是( )A、 B、 C、 D、6. 如图,若“马”所在的位置的坐标为(-2,-1),“象”所在位置的坐标为(-1,1),则“兵”所在位置的坐标为( )
A、①② B、②③ C、①③ D、②④5. 以为解的二元一次方程组是( )A、 B、 C、 D、6. 如图,若“马”所在的位置的坐标为(-2,-1),“象”所在位置的坐标为(-1,1),则“兵”所在位置的坐标为( )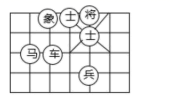 A、(-2,1) B、(-2,2) C、(1,-2) D、(2,-2)7. 袋里有若干个大小相同红球和白球,如果摸一红球得5分,摸一白球得1分. 那么总得分为分摸法有多少种?( )A、3 B、4 C、5 D、68. 下列说法中正确的有( )
A、(-2,1) B、(-2,2) C、(1,-2) D、(2,-2)7. 袋里有若干个大小相同红球和白球,如果摸一红球得5分,摸一白球得1分. 那么总得分为分摸法有多少种?( )A、3 B、4 C、5 D、68. 下列说法中正确的有( )①在同一平面内,不相交的两条直线必平行②过一点有且只有一条直线与已知直线垂直③相等的角是对顶角:④两条直线被第三条直线所截,所得的同位角相等⑤两条平行线被第三条直线所截,一对内错角的角平分线互相平行
A、4个 B、3个 C、2个 D、1个9. 如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )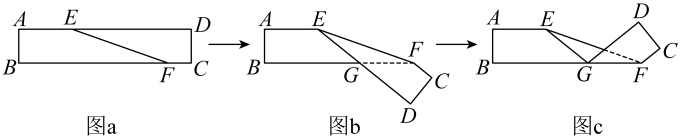 A、102° B、108° C、124° D、128°10. 如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2023个点的坐标为( )
A、102° B、108° C、124° D、128°10. 如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2023个点的坐标为( )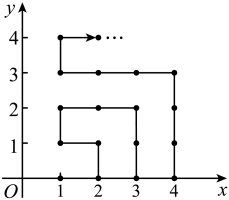 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若方程组是二元一次方程组,则“……”可以是 .12. 如图,小明利用两块相同的三角板,分别在三角板的边缘画直线AB和CD,并由此判定AB∥CD,这是根据.
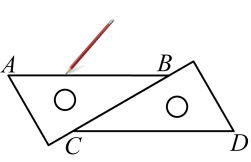 13. 已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为3,则点B的坐标是 .14. 比较大小: , (填、或).15. 方程的解是 .16. 若 , 则的立方根是 .17. 已如方程组和有相同的解.则的值是 .18. 已知直线 , 射线、分别平分 , , 两射线反向延长线交于点 , 请写出 , 之间的数量关系: .
13. 已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为3,则点B的坐标是 .14. 比较大小: , (填、或).15. 方程的解是 .16. 若 , 则的立方根是 .17. 已如方程组和有相同的解.则的值是 .18. 已知直线 , 射线、分别平分 , , 两射线反向延长线交于点 , 请写出 , 之间的数量关系: .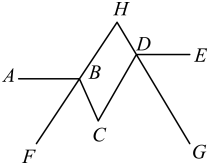
三、解答题
-
19. 计算:(1)、(2)、20. 在如图所示的直角坐标系中,解答下列问题:
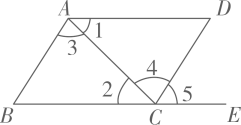
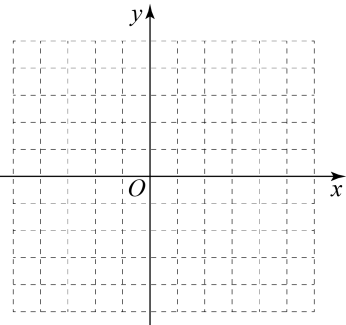 (1)、已知A(2,0),B(-1,-4),C(3,-3)三点,分别在坐标系中找出它们,并连接得到△ABC;(2)、将△ABC向上平移4个单位,得到△;(3)、求四边形的面积.21. 完成下面推理过程.如图:已知 , . 求证: .
(1)、已知A(2,0),B(-1,-4),C(3,-3)三点,分别在坐标系中找出它们,并连接得到△ABC;(2)、将△ABC向上平移4个单位,得到△;(3)、求四边形的面积.21. 完成下面推理过程.如图:已知 , . 求证: .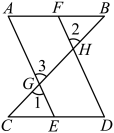
证明:(已知)
( )
( )(等量代换)
∴( )
▲ ( )
∵( )
( )
▲ ( )
( ).
22. 列方程组解应用题:为了丰富学生的课外体育活动,八年级2班需要购买排球和跳绳,根据下列对话,求出肖雨所购买的排球和跳绳的单价. 23. 如图,AB∥CD,E是CD上一点,AE交BC于点F,且∠ABE=∠DBC,∠ABC=∠AEB.
23. 如图,AB∥CD,E是CD上一点,AE交BC于点F,且∠ABE=∠DBC,∠ABC=∠AEB. (1)、试判断AE与BD的位置关系,并说明理由;(2)、若BE平分∠CBD,∠AEB=40°,求∠D的度数.24. 先阅读然后解答提出的问题:
(1)、试判断AE与BD的位置关系,并说明理由;(2)、若BE平分∠CBD,∠AEB=40°,求∠D的度数.24. 先阅读然后解答提出的问题:设a、b是有理数,且满足 , 求ba的值.
解:由题意得 ,
因为a、b都是有理数,所以a-3,b+2也是有理数,
由于是无理数,所以a-3=0,b+2=0,
所以a=3,b=-2, 所以 .
问题:设x、y都是有理数,且满足 , 求x+y的值.
25. 如图(1),直线与直线 , 分别交于点 , , 与互补.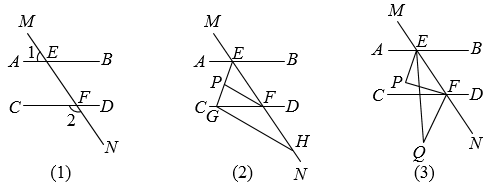 (1)、试判断直线与直线的位置关系,并说明理由;(2)、如图(2),与的角平分线交于点 , 延长线与交于点 , 点是上一点,且 , 试判断直线与的位置关系,并说明理由;(3)、如图(3),点为 , 之间一点, , 分别平分和 , 求与之间的数量关系.26. 如图,在平面直角坐标系中,四边形是长方形, , , , , 点A的坐标为 . 动点的运动速度为每秒个单位长度,动点的运动速度为每秒个单位长度,且 . 设运动时间为 , 动点、相遇则停止运动.
(1)、试判断直线与直线的位置关系,并说明理由;(2)、如图(2),与的角平分线交于点 , 延长线与交于点 , 点是上一点,且 , 试判断直线与的位置关系,并说明理由;(3)、如图(3),点为 , 之间一点, , 分别平分和 , 求与之间的数量关系.26. 如图,在平面直角坐标系中,四边形是长方形, , , , , 点A的坐标为 . 动点的运动速度为每秒个单位长度,动点的运动速度为每秒个单位长度,且 . 设运动时间为 , 动点、相遇则停止运动.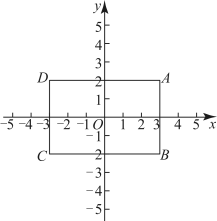
 (1)、 , ;(2)、动点 , 同时从点A出发,点沿长方形的边界逆时针方向运动,点沿长方形的边界顺时针方向运动,当为何值时、两点相遇?求出相遇时、所在位置的坐标;(3)、动点从点A出发,同时动点从点出发:
(1)、 , ;(2)、动点 , 同时从点A出发,点沿长方形的边界逆时针方向运动,点沿长方形的边界顺时针方向运动,当为何值时、两点相遇?求出相遇时、所在位置的坐标;(3)、动点从点A出发,同时动点从点出发:①若点、均沿长方形的边界顺时针方向运动,直接写出相遇时、所在位置的坐标;
②若点、均沿长方形的边界逆时针方向运动,直接写出相遇时、所在位置的坐标.