广东省深圳市2022-2023学年高二下学期数学期末模拟测试试卷

试卷更新日期：2023-06-26 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in Z | - 1 \leq x \leq 3} ， B = {x | x^{2} \geq 2 x}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 1 ， 2}$ B、 ${- 1 ， 0 ， 1}$ C、 ${- 1 ， 0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 2 ， 3}$

查看试题解析
2. 若 $(z + i) i = 4 - 7 i$ ，则复数z的虚部为（）

A、-5 B、5 C、7 D、-7

查看试题解析
3. 已知 $t a n θ = - 2$ ，则 $\frac{s i n (\frac{π}{2} + θ) + 2 s i n (π + θ)}{c o s (π - θ) + s i n (2 π - θ)}$ 的值为（）

A、-5 B、5 C、 $- \frac{5}{3}$ D、 $\frac{5}{3}$

查看试题解析
4. 过点 $(0 ， - 1)$ 的直线中，被圆 $x^{2} + y^{2} + 4 x - 4 y = 0$ 截得的弦最长的直线的方程是（）

A、 $3 x - 2 y - 2 = 0$ B、 $3 x + 2 y - 2 = 0$ C、 $3 x - 2 y + 2 = 0$ D、 $3 x + 2 y + 2 = 0$

查看试题解析
5. $(1 - x) (1 + x)^{5}$ 展开式中 $x^{3}$ 的系数是（）

A、0 B、5 C、15 D、20

查看试题解析
6. 函数 $f (x) = \frac{e^{x - 1}}{| x |}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
7. 在某项测试中，测量结果 $ξ$ 服从正态分布 $N (1 ， σ^{2}) (σ > 0)$ ，若 $P (1 < ξ < 2) = 0.3$ ，则 $P (ξ < 0) =$ （）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
8. 已知 $△ A B C$ 的内角A，B，C的对边分别为a，b，c， $△ A B C$ 的面积为 $4 \sqrt{3}$ ， $A = 6 0^{∘}$ ， $b^{2} + c^{2} = 3 b c$ ，则 $a =$ （）

A、4 B、 $4 \sqrt{2}$ C、8 D、 $8 \sqrt{2}$

查看试题解析

二、多选题

9. 关于函数 $f (x) = 2 s i n (2 x - \frac{13}{4} π)$ 的图象，下列说法正确的是（）

A、 $(\frac{π}{8} ， 0)$ 是曲线 $y = f (x)$ 的一个对称中心 B、 $x = \frac{5 π}{8}$ 是曲线 $y = f (x)$ 的一条对称轴 C、曲线 $y = 2 s i n 2 x$ 向左平移 $\frac{5}{8} π$ 个单位，可得曲线 $y = f (x)$ D、曲线 $y = 2 s i n 2 x$ 向右平移 $\frac{5}{8} π$ 个单位，可得曲线 $y = f (x)$

查看试题解析
10. 设有两条不同的直线m、n和两个不同的平面 $α$ 、 $β$ ，下列命题中错误的命题是（）

A、若 $m / / α$ ， $n / / α$ ，则 $m / / n$ B、若 $m \subset α$ ， $n \subset α$ ， $m / / β$ ， $n / / β$ ，则 $α / / β$ C、若 $m / / n$ ， $m \subset α$ ，则 $n / / α$ D、若 $α / / β$ ， $m \subset α$ ，则 $m / / β$

查看试题解析
11. 函数 $f (x) = a x^{3} + b x^{2} + c x + d (a ， b ， c ， d \in R)$ 的图象如图所示，则以下结论正确的有（）

A、 $b + c > 0$ B、 $b c > 0$ C、 $3 a + 2 b + c < 0$ D、 $a + b + c > 0$

查看试题解析
12. 已知函数 $y = f (x)$ 如下表所示，则下列结论错误的是（）

x

$0 < x < 2$

$2 \leq x < 4$

$4 \leq x < 6$

$6 \leq x \leq 8$

$f (x)$

1

2

3

4

A、 $f [f (4)] = 3$ B、 $f (x)$ 的值域是 ${1 ， 2 ， 3 ， 4}$ C、 $f (x)$ 的值域是 $[1 ， 4]$ D、 $f (x)$ 在区间 $[4 ， 8]$ 上单调递增

查看试题解析

三、填空题

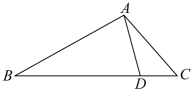
13. 已知 $△ A B C$ 中， $∠ B A C = 120 ° ， A B = 2 A C ， \vec{B D} = 4 \vec{D C} ， A D = \frac{2 \sqrt{3}}{5}$ ，则 $\vec{A D} \cdot \vec{B C} =$ ．

查看试题解析
14. 函数 $y = a^{x + 1} - 2 (a > 0 ， a \neq 1 ）$ 的图象恒过定点A，若点A在直线 $m x + n y + 1 = 0$ 上，其中 $m 、 n > 0$ ，则 $\frac{1}{m} + \frac{2}{n}$ 的最小值为．

查看试题解析
15. 已知甲袋中有3个白球和2个红球，乙袋中有2个白球和4个红球．若先随机取一只袋，再从该袋中先后随机取2个球，则在第一次取出的球是红球的前提下，第二次取出的球是白球的概率为．

查看试题解析
16. 下列命题中正确的命题有．（填序号）
①线性回归直线必过样本数据的中心点 $(\bar{x} ， \bar{y})$ ；②当相关性系数 $r > 0$ 时，两个变量正相关；

③如果两个变量的相关性越强，则相关性系数r就越接近于1；

④残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高；

⑤甲、乙两个模型的 $R^{2}$ 分别约为0.88和0.80，则模型乙的拟合效果更好．

查看试题解析

四、解答题

17. 设数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ 满足 $S_{n} = 2 a_{n} - a_{1}$ ，且 $a_{1}$ ， $a_{2} - 1$ ， $a_{3} - 3$ 成等比数列.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 ${\frac{1}{2} b_{n} + a_{n}}$ 是首项为1，公差为2的等差数列，求数列 ${b_{n}}$ 的通项公式与前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 在△ABC中，已知 $b = 5$ ， $c o s B = \frac{9}{16}$ ，再从条件①、条件②这两个条件中选择一个作为已知．
条件①： $c o s C = \frac{1}{8}$ ；条件②： $a = 4$ ．

(1)、求 $s i n A$ ；

(2)、求△ABC的面积．

查看试题解析
19. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = B C = C C_{1} = \sqrt{2} ， A B ⊥ B C$ .

(1)、求证： $A C_{1} ⊥ B_{1} C$ ；

(2)、求 $B_{1} C$ 与平面 $A A_{1} C_{1} C$ 所成的角的大小.

查看试题解析

20. 浙江省是第一批新高考改革省份，取消文理分科，变成必考科目和选考科目．其中必考科目是语文、数学、外语，选考科目由考生在思想政治、历史、地理、物理、化学、生物、技术7个科目中自主选择其中3个科目参加等级性考试．为了调查学生对物理、化学、生物的选考情况，从镇海中学高三在物理、化学、生物三个科目中至少选考一科的学生中随机抽取100名学生进行调查，他们选考物理、化学、生物的科目数及人数统计如表：

选考物理、化学、生物的科目数	1	2	3
人数	20	40	40

参考公式： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．

附表：

$α$	0.10	0.05	0.010	0.001
$x_{α}$	2.706	3.841	6.635	10.828

(1)、从这100名学生中任选2名，求他们选考物理、化学、生物科目数相等的概率；

(2)、从这100名学生中任选2名，记X表示这2名学生选考物理、化学、生物的科目数之差的绝对值，求随机变量X的数学期望；

(3)、学校还调查了这100位学生的性别情况，研究男女生中纯理科生大概的比例，得到的数据如下表：（定文同时选考物理、化学、生物三科的学生为纯理科生）

性别	纯理科生	非纯理科生	总计
男性	30
女性		5
总计			100

请补齐表格，并说明依据小概率值 $α = 0.05$ 的独立性检验，能否认为同时选考物理、化学、生物三科与学生性别有关．

查看试题解析

21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $A (- 2 ， - 1)$ ，长轴长为 $4 \sqrt{2}$ .

(1)、求椭圆 $C$ 的方程及其焦距；

(2)、直线 $l ： y = k x + m$ 与椭圆 $C$ 交于不同的两点 $M ， N$ ，直线 $A M ， A N$ 分别与直线 $x = - 4$ 交于点 $P ， Q$ ， $O$ 为坐标原点且 $| O P | = | O Q |$ ，求证：直线 $l$ 过定点，并求出定点坐标.

查看试题解析
22. 已知函数 $f (x) = {(1 + x)}^{a}$ ， $g (x) = 1 + a x$ ， $(a \in R)$ ；

(1)、当 $a = 3$ 时，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、若正数a使得 $f (x) ≥ g (x)$ 对 $x \in [0 ， + \infty)$ 恒成立，求a的取值范围.

查看试题解析

x	$0 < x < 2$	$2 \leq x < 4$	$4 \leq x < 6$	$6 \leq x \leq 8$
$f (x)$	1	2	3	4