广西玉林市2023届高三下学期理数第三次模拟考试试卷
试卷更新日期:2023-06-26 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、或 B、 C、 D、2. 已知复数 , 则( )A、2 B、 C、 D、13. 我国在2020年开展了第七次全国人口普查,并于2021年5月11日公布了结果.自新中国成立以来,我国共进行了七次全国人口普查,下图为我国历次全国人口普查人口性别构成及总人口性别比(以女性为100,男性相对女性的比例)统计图,则下列说法错误的是( )
 A、近三次全国人口普查总人口性别比呈递减趋势 B、我国历次全国人口普查总人口数呈逐次递增 C、第五次全国人口普查时,我国总人口数不足12亿 D、第七次人口普查时,我国总人口性别比最低4. 已知正项等比数列}满足为与的等比中项,则( )A、 B、 C、 D、25. 已知 , 且 , 则( )A、 B、 C、 D、6. 已知双曲线的一条渐近线方程为 , 则双曲线的离心率为( )A、2 B、 C、 D、7. 函数的大致图象是( )A、
A、近三次全国人口普查总人口性别比呈递减趋势 B、我国历次全国人口普查总人口数呈逐次递增 C、第五次全国人口普查时,我国总人口数不足12亿 D、第七次人口普查时,我国总人口性别比最低4. 已知正项等比数列}满足为与的等比中项,则( )A、 B、 C、 D、25. 已知 , 且 , 则( )A、 B、 C、 D、6. 已知双曲线的一条渐近线方程为 , 则双曲线的离心率为( )A、2 B、 C、 D、7. 函数的大致图象是( )A、 B、
B、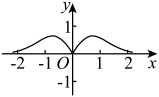 C、
C、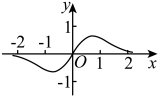 D、
D、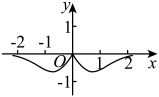 8. 某几何体的三视图如图所示(单位:),则该几何体的体积是( )
8. 某几何体的三视图如图所示(单位:),则该几何体的体积是( ) A、 B、 C、 D、9. 已知 , , 则( )A、 B、 C、 D、10. 已知抛物线的焦点为 , 准线为 , 一圆以为圆心且与相切,若该圆与抛物线交于点 , 则的值为( )A、或 B、-2或2 C、-2 D、11. 如图,有一个水平放置的透明无盖的正三棱柱容器,所有棱长都为 , 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为 , 如果不计容器的厚度,则球的体积为( )
A、 B、 C、 D、9. 已知 , , 则( )A、 B、 C、 D、10. 已知抛物线的焦点为 , 准线为 , 一圆以为圆心且与相切,若该圆与抛物线交于点 , 则的值为( )A、或 B、-2或2 C、-2 D、11. 如图,有一个水平放置的透明无盖的正三棱柱容器,所有棱长都为 , 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为 , 如果不计容器的厚度,则球的体积为( ) A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、二、填空题
-
13. 若 , 则的最小值是 .14. 的展开式中的系数为 .15. 椭圆的左、右焦点分别为 , 离心率为为椭圆的左顶点,且 , 过原点的直线交椭圆于两点,则的取值范围为.16. 给出下列命题:(1)函数不是周期函数;(2)函数在定义域内为增函数;(3)函数的最小正周期为;(4)函数 , 的一个对称中心为 . 其中正确命题的序号是 .
三、解答题
-
17. 在中,内角 , , 所对的边分别为、、 , 已知.(1)、求角的大小;(2)、若 , , 求的面积.18. 年月日,中国疾控中心成功分离中国首株新型冠状病毒毒种,月日时分,重组新冠疫苗获批启动临床试验.月日,中国新冠病毒疫苗进入期临床试验截至月日,全球当前有大约种候选新冠病毒疫苗在研发中,其中至少有种疫苗正处于临床试验阶段现有、、三个独立的医疗科研机构,它们在一定时期内能研制出疫苗的概率分别是、、 . 求:(1)、他们都研制出疫苗的概率;(2)、他们都失败的概率;(3)、他们能够研制出疫苗的概率.19. 如图,三棱柱的底面是正三角形,侧面是菱形,平面平面 , , , 分别是棱 , , 的中点.
 (1)、证明:平面;(2)、若 , , 求点到平面的距离.20. 已知抛物线C1:与椭圆C2:()有公共的焦点,C2的左、右焦点分别为F1 , F2 , 该椭圆的离心率为.
(1)、证明:平面;(2)、若 , , 求点到平面的距离.20. 已知抛物线C1:与椭圆C2:()有公共的焦点,C2的左、右焦点分别为F1 , F2 , 该椭圆的离心率为. (1)、求椭圆C2的方程;(2)、如图,若直线l与x轴,椭圆C2顺次交于P,Q,R(P点在椭圆左顶点的左侧),且∠PF1Q与∠PF1R互为补角,求△F1QR面积S的最大值.
(1)、求椭圆C2的方程;(2)、如图,若直线l与x轴,椭圆C2顺次交于P,Q,R(P点在椭圆左顶点的左侧),且∠PF1Q与∠PF1R互为补角,求△F1QR面积S的最大值.