吉林省梅河口市2023届高三下学期6月第七次数学模拟考试试卷
试卷更新日期:2023-06-26 类型:高考模拟
一、单选题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个选项是符合题目要求的,请仔细审题,认真做答
-
1. 若复数满足 , 其中为虚数单位,则( )A、0 B、-1 C、 D、12. 已知集合 , 则( )A、 B、 C、 D、3. 设非零向量满足 , 则在上的投影向量为( )A、 B、 C、 D、4. 从2至8的7个整数中随机取2个不同的数,若取出的2个数互质,则取出两个数都是奇数的概率为( )A、 B、 C、 D、5. 在平面直角坐标系中,直线与双曲线交于两点,是该双曲线的焦点,且满足 , 若的面积为 , 则双曲线的离心率为( )A、 B、 C、 D、56. 若球是正三棱锥的外接球, , 点在线段上, , 过点作球的截面,则所得的截面中面积最小的截面的面积为( )A、 B、 C、 D、7. 若函数有两个极值点 , 且 , 则( )A、 B、 C、 D、8. 已知则( )A、 B、 C、 D、
二、多选题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项是等合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分,请仔细审题,认真皕答
-
9. 十六世纪中叶,英国数学家雷科德在《励智石》一书中首先把“=”作为等号使用,后来英国数学家哈里奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若 , 则下列说法不成立的是( )A、若且 , 则 B、若 , 则 C、若 , 则 D、若且 , 则10. 若函数同时满足以下条件:①是函数的零点,且;② , 有 , 则( )A、 B、将的图象向左平移个单位长度得到的图象解析式为 C、在上单调递减 D、直线是曲线的一条对称轴11. 已知点是抛物线的焦点,为坐标原点,直线与抛物线交于两点,抛物线的准线与轴交于点 , 下列说法正确的是( )A、若过抛物线的焦点 , 则直线斜率之积为定值 B、若抛物线上的点到点的距离为4,则抛物线的方程为 C、以为直径的圆与准线相切 D、直线过点且交于不同的两点,则12. 已知正方体的棱长为为空间中任一点,则下列结论中正确的是( )A、若为线段上任一点,则与所成角的余弦值范围为 B、若为正方形的中心,则三棱锥外接球的体积为 C、若在正方形内部,且 , 则点轨迹的长度为 D、若三棱锥的体积为恒成立,点轨迹的为圆的一部分
三、填空题:本大题共4小题,每小题5分,共20分,请仔细审题,认真做答
-
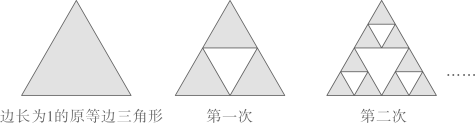
13. 的展开式中,的系数为.14. 由直线上一点向圆引切线,则切线长的最小值为.15. 已知函数在区间上存在零点,则的最小值为.16. 如图,将一个边长为1的正三角形分成四个全等的正三角形,第一次挖去中间的一个小三角形,将剩下的三个小正三角形,再分别从中间挖去一个小三角形,保留它们的边,重复操作以上做法,得到的集合为谢尔宾斯基三角形.设是第次挖去的小三角形面积之和(如是第1次挖去的中间小三角形面积,是第2次挖去的三个小三角形面积之和),则;若操作次后剩余部分面积不大于原图面积的一半,则的最小值为.
四、解答题:本大题共6小题,共70分,请仔细审题,认真做答
-
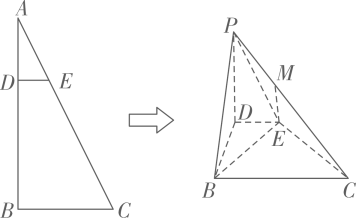
17. 如图所示,在直角三角形中, , , 将沿折起到的位置,使平面平面 , 点满足.
 (1)、证明:;(2)、求二面角的余弦值.18. 记的内角的对边分别为 , 分别以为边长的三个正三角形的面积依次为 , 已知.(1)、求的面积;(2)、若 , 求.19. 为数列的前项和,已知 , 且.(1)、求数列的通项公式;(2)、数列依次为: , 规律是在和中间插入项,所有插入的项构成以3为首项,3为公比的等比数列,求数列的前100项的和.20. 某学校离三年级开学之初增加早自习,早饭在校食堂就餐人数增多,为了缓解就餐压力,学校在原有一个餐厅的基础上增加了一个餐厅,分别记做餐厅甲和餐厅乙,经过一周左右统计调研分析:前一天选择餐厅甲就餐第二天选择餐厅甲就餐的概率是 , 择餐厅乙就餐的概率为 , 前一天选择餐厅乙就餐第二天选择餐厅乙就餐的概率是 , 选择餐厅甲就餐的概率也为 , 如此往复.假设学生第一天选择餐厅甲就餐的概率是 , 择餐厅乙就餐的概率是 , 记某同学第天选择甲餐厅就餐的概率为.(1)、记某班级的3位同学第二天选择餐厅甲的人数为 , 求的分布列,并求;(2)、请写出的通项公式;
(1)、证明:;(2)、求二面角的余弦值.18. 记的内角的对边分别为 , 分别以为边长的三个正三角形的面积依次为 , 已知.(1)、求的面积;(2)、若 , 求.19. 为数列的前项和,已知 , 且.(1)、求数列的通项公式;(2)、数列依次为: , 规律是在和中间插入项,所有插入的项构成以3为首项,3为公比的等比数列,求数列的前100项的和.20. 某学校离三年级开学之初增加早自习,早饭在校食堂就餐人数增多,为了缓解就餐压力,学校在原有一个餐厅的基础上增加了一个餐厅,分别记做餐厅甲和餐厅乙,经过一周左右统计调研分析:前一天选择餐厅甲就餐第二天选择餐厅甲就餐的概率是 , 择餐厅乙就餐的概率为 , 前一天选择餐厅乙就餐第二天选择餐厅乙就餐的概率是 , 选择餐厅甲就餐的概率也为 , 如此往复.假设学生第一天选择餐厅甲就餐的概率是 , 择餐厅乙就餐的概率是 , 记某同学第天选择甲餐厅就餐的概率为.(1)、记某班级的3位同学第二天选择餐厅甲的人数为 , 求的分布列,并求;(2)、请写出的通项公式;