山东省德州市2022-2023学年高一下学期6月数学阶段测试试卷
试卷更新日期:2023-06-26 类型:月考试卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
-
1. 已知向量、满足 , , 且 , 则( )A、 B、 C、 D、22. 若复数 , 则的虚部为( )A、 B、 C、 D、3. 在中,内角A,B,C所对的边分别为a,b,c,的面积为 , , , 则( )A、 B、 C、4 D、4. 已知l值直线, , 是两个不同平面,下列命题中的真命题是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则5. 下列各式化简结果为的是( )A、 B、 C、 D、6. 如图所示,在直三棱柱中,棱柱的侧面均为矩形, , , , P是上的一动点,则的最小值为( )
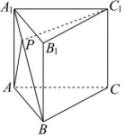 A、 B、2 C、 D、7. 如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是( )
A、 B、2 C、 D、7. 如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是( )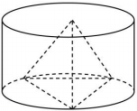 A、 B、 C、 D、8. 已知 , (),若函数在区间内存不住对称轴,则w的范围为( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知 , (),若函数在区间内存不住对称轴,则w的范围为( )A、 B、 C、 D、二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 在中,若 , 下列结论中正确的有( )A、 B、时钝角三角形 C、的最大内角是最小内角的2倍 D、若 , 则外接圆的半径为10. 陀螺是中国民间最早的娱乐工具之一,也作陀罗,闽南语称作“干乐”,北方叫作“冰尜(gá)”或“打老牛”.传统古陀螺大致是木制或铁制的倒圆锥形.现有一圆锥形陀螺(如图所示),其底面半径为3,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点S滚动,当圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( )
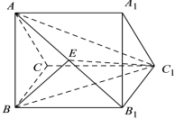
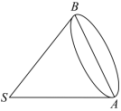 A、圆锥的母线长为 9 B、圆锥的表面积为 C、圆锥的侧面展开图(扇形)的圆心角为60° D、圆锥的体积为11. 如图,正方体的棱长为1,线段上有两个动点 , , 且 , 则下列结论中正确的是( )
A、圆锥的母线长为 9 B、圆锥的表面积为 C、圆锥的侧面展开图(扇形)的圆心角为60° D、圆锥的体积为11. 如图,正方体的棱长为1,线段上有两个动点 , , 且 , 则下列结论中正确的是( )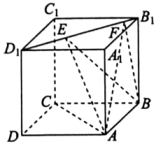 A、 B、平面 C、三棱锥的体积为定值 D、的面积与的面积相等12. 如图,在正方体中,点P在线段上运动时,下列命题正确的是( )
A、 B、平面 C、三棱锥的体积为定值 D、的面积与的面积相等12. 如图,在正方体中,点P在线段上运动时,下列命题正确的是( )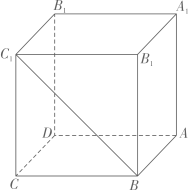 A、三棱锥的体积不变 B、直线CP与直线所成角的取值范围为 C、直线AP与平面所成角的大小不变 D、二面角的大小不变
A、三棱锥的体积不变 B、直线CP与直线所成角的取值范围为 C、直线AP与平面所成角的大小不变 D、二面角的大小不变三、填空题:本题共4小题,每小题5分,共20分
-
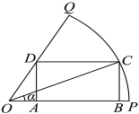
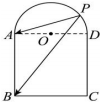
13. 函数的最小正周期为 .14. 在中,a,b,c分别是角A,B,C的对边,若 , , 则 .15. 已知三棱锥的体积为6,且 . 则该三棱锥外接球的表面积为 .16. 如图,已知正方形ABCD的边长为2,点P是半圆O上一点(包括端点A,D),则的取值范围是 .
四、解答题:本小题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
-
17. 如图,在圆内接四边形ABCD中, , , , 的面积为 .
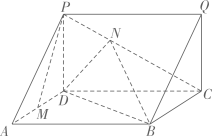
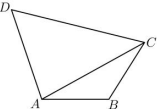 (1)、求AC;(2)、求 .18. 已知向量 , , .(1)、若 , 求t的值;(2)、若与的夹角为锐角,求t的取值范围.19. 如图,在四棱锥中,底面ABCD是平行四边形, , 点E是PB的中点.
(1)、求AC;(2)、求 .18. 已知向量 , , .(1)、若 , 求t的值;(2)、若与的夹角为锐角,求t的取值范围.19. 如图,在四棱锥中,底面ABCD是平行四边形, , 点E是PB的中点.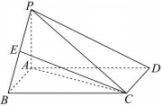 (1)、求证:平面EAC;(2)、若 , , , 求点P到平面AEC的距离.
(1)、求证:平面EAC;(2)、若 , , , 求点P到平面AEC的距离.