浙江省温州二中2022-2023学年八年级（下）期中数学试卷

试卷更新日期：2023-06-25 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 下列标志中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列是一元二次方程的是（）

A、 $2 x + 1 = 0$ B、 $x + y = 5$ C、 $x^{2} + 3 x + 2 = 0$ D、 $x + \frac{1}{x} = 2$

查看试题解析
3. 甲、乙、丙三个人进行排球垫球测试，他们的平均成绩相同，方差分别是：S_甲²＝0.62，S_乙²＝0.45，S_丙²＝0.53，成绩最稳定的是（）

A、甲 B、乙 C、丙 D、三个都一样

查看试题解析
4. 如图，四边形 $A B C D$ 的对角线交于点 $O$ ，下列不能判定其为平行四边形的是（）

A、 $A B = C D ， A D = B C$ B、 $A B ∥ C D ， A B = C D$ C、 $O A = O C ， O B = O D$ D、 $A B ∥ C D ， A D = B C$

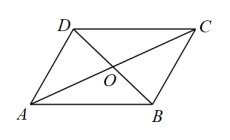查看试题解析
5. 用反证法证明“若a＜3，则a²＜9”时，应假设（）

A、|a|≥3 B、|a|＞3 C、a²≥9 D、a²＞9

查看试题解析
6. 若一个n边形内角和为 $540 °$ ，则n的值为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 如图，已知实数a在数轴上的对应点位置如图所示，则化简 $\sqrt{(a - 2)^{2}}$ 的结果是（）

A、a-2 B、-a-2 C、1 D、2-a

查看试题解析
8. 如图， $▱ A B C D$ 中， $A B = 12 ， P C = 4 ， A P$ 是 $∠ D A B$ 的平分线，则 $▱ A B C D$ 周长为（）

A、20 B、24 C、32 D、40

查看试题解析
9. 如图，某景区内有一块长方形油菜花田地（单位：m），现在其中修建观花道（阴影部分）供游人赏花，要求观花道面积是30．设观花道的直角边为x，则可列方程为（）

A、（10+x）（9+x）＝30 B、（10+x）（9+x）＝60 C、（10-x）（9-x）＝30 D、（10-x）（9-x）＝60

查看试题解析
10. 如图，含 $30 °$ 角的三角尺（ $△ A B C$ ）的长直角边与含 $45 °$ 角的三角尺（ $△ A C D$ ）的斜边恰好重合， $A B$ 交 $C D$ 于点E．P，Q分别是边 $A C$ ， $B C$ 上的动点，当四边形 $E P Q B$ 为平行四边形时， $▱ E P Q B$ 的面积3，则线段 $C E$ 的长是（）

A、 $\sqrt{3}$ B、 $\sqrt{6}$ C、3 D、 $2 \sqrt{3}$

查看试题解析

二、填空题（本题有8小题，每小题4分，共32分）

11. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 100 °$ ，则 $∠ A =$ ．

查看试题解析
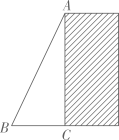
12. 使式子 $\sqrt{x - 2}$ 有意义，则x的取值范围为．

查看试题解析
13. 若用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，将其配方为 ${(x + b)}^{2} = c$ 的形式，则 $c =$ ．

查看试题解析
14. 在平面直角坐标系中，点P（-5，5）与点Q（5，m）关于原点对称，则m＝．

查看试题解析
15. 如图，大坝横截面迎水坡AB的坡比为2：1，若坝高AC为12（m），则迎水坡AB的长为（m）．

查看试题解析
16. 如图，在Rt△ABC中，∠B＝90°，∠ACB＝30°，BC＝3．点P为BC边上任意一点，连结PA，以PA，PC为邻边作▱PAQC，连结PQ，则PQ的最小值为．

查看试题解析
17. 已知关于x的一元二次方程x²-2x+3m＝0有实数根，设此方程的一个实数根为t，令y＝t²-2t+4m+1，则y的取值范围为．

查看试题解析
18. 如图1是雨伞的结构示意图．OP是伞柄，OM，AB，CD是伞骨．已知点A，C分别是OM，AB的中点．CD＝ $\sqrt{7}$ （dm），点B，D在OP上滑动时，可将雨伞打开或收拢．当OP与水平面垂直时打开雨伞，雨伞能罩住的水平面大小可近似地看成一个圆．如图2，当雨伞完全打开时，∠ABD＝90°；再将雨伞收拢到如图3，此时B′D′＝1（dm），且点C′到OP的距离恰好等于图2中BD的长．则伞骨AB的长为（dm），设图2中能罩住的水平面面积是S₁ ，图3中能罩住的水平面面积是S₂ ，则 $\frac{S_{1}}{S_{2}}$ ＝．

查看试题解析

三、解答题（本题有6小题，共58分）

19.

(1)、计算： $(\sqrt{3})^{2} - \sqrt{24} \times \sqrt{\frac{1}{3}}$ ；

(2)、解方程：x²-4x＝-3．

查看试题解析

20. 甲，乙两名队员参加训练，每人射击10次的成绩分别被制成下列两个统计图：

根据以上信息，整理分析数据如下：

	平均成绩环	众数/环	中位数/环	方差/环²
甲	a	7	7	1.2
乙	7	b	c	4.6

(1)、写出表格中a，b，c的值：

a =

，

b =

，

c =

；

(2)、根据以上统计数据，你会选择谁参加比赛，请说明理由．

查看试题解析

21. 如图，在6×6网格中，每个小正方形的边长为1，已知点A，B在格点上，请仅用无刻度直尺，且不能用直尺中的直角，画出符合要求的格点图形．

(1)、在图甲中画出以线段AB为对角线的▱AMBN；

(2)、在图乙中画出以线段AB为边的▱ABCD，且使其面积最大．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O． $B D = 2 A D$ ， E，F，G分别是 $O C$ ， $O D$ ， $A B$ 的中点．

(1)、求证： $B E ⊥ A C$ ；

(2)、若 $E F = 2$ ，求 $E G$ 的长．

查看试题解析

23. 根据以下素材，探索完成任务．

素材1	某校统一安装了日光灯，日光灯中最易损坏的是灯管和镇流器．
素材2	该校后勤部准备补进灯管和镇流器共400件．批发市场灯管的单价为30元，镇流器的单价为80元．商家为了促销且保证有一定的利润，当镇流器购买数量超过80件时，每多购买1件，单价下降1元，但单价不低于50元．
问题解决
任务1	若镇流器补进90件，则学校补进镇流器和灯管共多少元？
任务2	设镇流器补进x件，若 $80 \leq x \leq 110$ ，刚补进镇流器的单价为 ▲ 元，补进灯管的总价为 ▲ （用含x的代数式表示）；
任务3	若学校后勤部补进镇流器和灯管共花15000元，求补进镇流器多少件？

查看试题解析

24. 如图1，在△ABC中，AB＝AC＝5，BC＝6．点D是BC边上的动点，连结AD，将△ADC绕点A旋转至△AEB，使点C与点B重合，连结DE交AB于点F．

(1)、当点D为BC中点时，线段DE＝；

(2)、如图2，作EG∥BC交AB于点G，连结CG交AD于点H．求证：四边形CDEG是平行四边形；

(3)、在（2）的条件下：
①若∠CAD＝26°，求∠CGE的度数；
②连接FH，当S_△_AFH＝S_△_BDE时，S_△_AED：S_四边形_AEBC＝ ▲ ．

查看试题解析