广东省深圳市龙岗区八年级2022-2023学年下册数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、3. 下列不等式组的解集,在数轴上表示为如图所示的是( )
2. 若 ,则下列式子一定成立的是( )A、 B、 C、 D、3. 下列不等式组的解集,在数轴上表示为如图所示的是( ) A、 B、 C、 D、或4. 四个三角形的边长分别是①2,3,4;②3,4,5;③5,6,7;④5,12,13.其中直角三角形是( )A、①② B、①③ C、②④ D、③④5. 已知点在第四象限,则的取值范围是( )A、 B、 C、 D、6. 如图,在中,和的平分线交于点 , 过点作交于 , 交于 , 若 , 则线段的长为( )
A、 B、 C、 D、或4. 四个三角形的边长分别是①2,3,4;②3,4,5;③5,6,7;④5,12,13.其中直角三角形是( )A、①② B、①③ C、②④ D、③④5. 已知点在第四象限,则的取值范围是( )A、 B、 C、 D、6. 如图,在中,和的平分线交于点 , 过点作交于 , 交于 , 若 , 则线段的长为( ) A、 B、 C、 D、7. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、8. 如图,沿直角边所在的直线向右平移得到 , 下列结论中错误的是
A、 B、 C、 D、7. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、8. 如图,沿直角边所在的直线向右平移得到 , 下列结论中错误的是 ( )
( )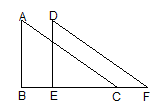 A、≌ B、 C、 D、9. 如图,是正内的一点,若将绕点旋转到 , 则的度数是( )
A、≌ B、 C、 D、9. 如图,是正内的一点,若将绕点旋转到 , 则的度数是( )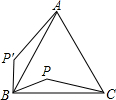 A、 B、 C、 D、10. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( )
A、 B、 C、 D、10. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(本大题共5小题,共15.0分)
-
11. 如果等腰三角形的两边长分别是2、7,那么三角形的周长是 .12. 如图,在中, , 的垂直平分线交于点 , 交边于点 , 的周长等于 , 则的长等于 .
 13. 如图,已知函数和的图象交于点 , 点的横坐标为 , 则关于的不等式的解集是 .
13. 如图,已知函数和的图象交于点 , 点的横坐标为 , 则关于的不等式的解集是 . 14. 如图,将线段平移到线段的位置,则的值为 .
14. 如图,将线段平移到线段的位置,则的值为 .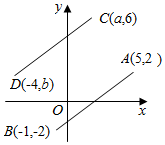 15. 如图,的两直角边 , 长分别为 , , 其三条角平分线交于点 , 将分为三个三角形,则:: .
15. 如图,的两直角边 , 长分别为 , , 其三条角平分线交于点 , 将分为三个三角形,则:: .
三、解答题(本大题共7小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
16. 解不等式: , 并把解集在数轴上表示出来.
 17. 解不等式组: .18. 如图,已知 , , , 为上一点,且到、两点的距离相等.
17. 解不等式组: .18. 如图,已知 , , , 为上一点,且到、两点的距离相等. (1)、用直尺和圆规,作出点的位置不写作法,保留作图痕迹;(2)、连结 , 若 , 求的度数.19. 如图,在等边三角形中,点 , 分别在边 , 上,且 , 过点作 , 交的延长线于点 .
(1)、用直尺和圆规,作出点的位置不写作法,保留作图痕迹;(2)、连结 , 若 , 求的度数.19. 如图,在等边三角形中,点 , 分别在边 , 上,且 , 过点作 , 交的延长线于点 . (1)、求的度数;(2)、若 , 求的长.20. 在平面直角坐标系中的位置如图所示,小正方形的边长为个单位.
(1)、求的度数;(2)、若 , 求的长.20. 在平面直角坐标系中的位置如图所示,小正方形的边长为个单位.
⑴作关于点成中心对称的 .
⑵将向右平移个单位,作出平移后的 .
⑶在轴上求作一点 , 使的值最小,求经过点和点的一次函数关系式,并求出点的坐标.
21. 某商店销售台型和台型电脑的利润为元,销售台型和台型电脑的利润为元.(1)、求每台型电脑和型电脑的销售利润各多少元;(2)、该商店计划一次购进两种型号的电脑共台,其中型电脑的进货量不超过型电脑的倍,设购进型电脑台,这台电脑的销售总利润为元.①求关于的函数关系式;
②该商店购进型、型电脑各多少台,才能使销售总利润最大?
22. 已知和都是等腰直角三角形, . (1)、如图:连 , , 求证:≌;(2)、若将绕点顺时针旋转,当点 , , 恰好在同一条直线上时,如图所示,线段 , 与交点为 , 若 , , 求出线段的长;(3)、若将绕点顺时针旋转,当点恰好落在边上时,如图所示,与交点为 , 求证: .
(1)、如图:连 , , 求证:≌;(2)、若将绕点顺时针旋转,当点 , , 恰好在同一条直线上时,如图所示,线段 , 与交点为 , 若 , , 求出线段的长;(3)、若将绕点顺时针旋转,当点恰好落在边上时,如图所示,与交点为 , 求证: .