浙江省杭州市拱墅区重点中学2022-2023学年八年级下册数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式是最简二次根式的是( )A、 B、 C、 D、3. 用配方法解方程时,配方结果正确的是( )A、 B、 C、 D、4. 用反证法证明命题“三角形中必有一个内角小于或等于”时,首先应该假设( )A、三角形中每个内角都大于 B、三角形中至少有一个内角大于 C、三角形中每个内角都大于或等于 D、三角形中每一个内角都小于成等于5. 若样本 , , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、中位数变小,方差不变 D、众数不变,方差为6. 如图,四边形的四个顶点分别在矩形的边和对角线上,已知 , 下列条件能使四边形是平行四边形的是( )
2. 下列各式是最简二次根式的是( )A、 B、 C、 D、3. 用配方法解方程时,配方结果正确的是( )A、 B、 C、 D、4. 用反证法证明命题“三角形中必有一个内角小于或等于”时,首先应该假设( )A、三角形中每个内角都大于 B、三角形中至少有一个内角大于 C、三角形中每个内角都大于或等于 D、三角形中每一个内角都小于成等于5. 若样本 , , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、中位数变小,方差不变 D、众数不变,方差为6. 如图,四边形的四个顶点分别在矩形的边和对角线上,已知 , 下列条件能使四边形是平行四边形的是( ) A、 B、 C、 D、7. 杭州地铁号线于2022年2月21日实现试运行,从星桥站至潮王路站共设计了1482种往返车票,则这段线路有多少个站点?设这段线路有个站点,根据题意下面列出的方程正确的是( )A、 B、 C、 D、8. 如图,小明在作线段的垂直平分线时,进行了如下操作:
A、 B、 C、 D、7. 杭州地铁号线于2022年2月21日实现试运行,从星桥站至潮王路站共设计了1482种往返车票,则这段线路有多少个站点?设这段线路有个站点,根据题意下面列出的方程正确的是( )A、 B、 C、 D、8. 如图,小明在作线段的垂直平分线时,进行了如下操作:
分别以点 , 为圆心,以大于长为半径画弧,两弧交于点 , ;
作直线根据小明的作图步骤可知四边形的形状一定是( )
A、矩形 B、菱形 C、正方形 D、梯形9. 如图,平行四边形的周长是 , 对角线与交于点 , , 是中点,的周长比的周长多 , 则的长度为( ) A、 B、 C、 D、10. 对于一元二次方程 , 下列说法:
A、 B、 C、 D、10. 对于一元二次方程 , 下列说法:若 , 则方程必有一根为;
若方程有两个不相等的实根,则方程无实根;
若方程两根为 , 且满足 , 则方程 , 必有实根 , ;
若是一元二次方程的根,则 .
其中正确的( )
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 若二次根式在实数范围内有意义,则的取值范围是 .12. 甲、乙、丙、丁四名学生最近次数学考试平均分都是分,方差 , , , , 则这四名学生的数学成绩最稳定的是 .13. 若a是一元二次方程的一个根,则的值是 .14. 如图,的周长为 , 以它的各边的中点为顶点作 , 再以各边的中点为顶点作 , 再以各边的中点为顶点作 , 如此下去,则的周长为 .
 15. 如图,已知的面积为 , 点在线段上,点在线段的延长线上,且 , 四边形是平行四边形,则图中阴影部分的面积是 .
15. 如图,已知的面积为 , 点在线段上,点在线段的延长线上,且 , 四边形是平行四边形,则图中阴影部分的面积是 .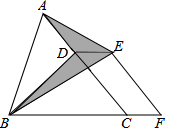 16. 如图,在正方形中,为的中点,点在边上,且则 , .
16. 如图,在正方形中,为的中点,点在边上,且则 , .
三、解答题(本大题共7小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、;(2)、 .19. 如图,在平行四边形中, , 分别平分和 , 交边于点 , , 线段 , 相交于点 .
 (1)、求证:;(2)、若 , 求的长.20. 在学校举办的“读书月”活动中,八年级班的小红调查了班级里所有同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:
(1)、求证:;(2)、若 , 求的长.20. 在学校举办的“读书月”活动中,八年级班的小红调查了班级里所有同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题: (1)、这次调查获取的样本数据的众数为元,中位数为元;(2)、计算这次调查获取的样本数据的平均数;(3)、若该校八年级共有学生人,根据调查数据,估计该校八年级学生本学期购买课外书共花费了多少元?21. 如图,在中, , 平分交于点 , 点在线段上,点在的延长线上,且 , 连接 , , , .
(1)、这次调查获取的样本数据的众数为元,中位数为元;(2)、计算这次调查获取的样本数据的平均数;(3)、若该校八年级共有学生人,根据调查数据,估计该校八年级学生本学期购买课外书共花费了多少元?21. 如图,在中, , 平分交于点 , 点在线段上,点在的延长线上,且 , 连接 , , , . (1)、求证:四边形是菱形;(2)、若 , , , 求和的长.22. 如图 , 用篱笆靠墙围成矩形花圃 , 一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为 , 篱笆长为 , 设平行于墙的边长为 .
(1)、求证:四边形是菱形;(2)、若 , , , 求和的长.22. 如图 , 用篱笆靠墙围成矩形花圃 , 一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为 , 篱笆长为 , 设平行于墙的边长为 .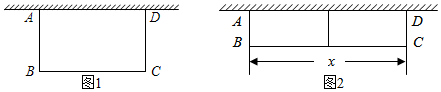 (1)、若围成的花圃面积为时,求的长;(2)、如图 , 若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为 , 请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.23. 如图,有一张矩形纸条 , , , 点 , 分别在边 , 上,现将四边形沿折叠,使点 , 分别落在点 , 上.
(1)、若围成的花圃面积为时,求的长;(2)、如图 , 若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为 , 请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.23. 如图,有一张矩形纸条 , , , 点 , 分别在边 , 上,现将四边形沿折叠,使点 , 分别落在点 , 上. (1)、当点恰好落在边上时,
(1)、当点恰好落在边上时,证明:是等腰三角形;
求线段的长;
(2)、点从点向点运动的过程中,若边线段与边交于点 ,求此运动过程中,的最大值;
请直接写出点相应运动的路径长.