黑龙江省哈尔滨市2022-2023学年七年级下册数学六月份月考试卷

试卷更新日期：2023-06-25 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列方程是二元一次方程的是（）。

A、 $2 x - y = 2$ B、 $x y = 1$ C、 $x^{2} - x + 1 = 0$ D、 $\frac{1}{x} + 2 y = 5$

查看试题解析
2. 下列各组线段为边，能构成三角形的是（）。

A、2，3，6 B、3，4，8 C、2，7，9 D、5，6，10

查看试题解析
3. 一元一次不等式组 ${\begin{array}{l} 2 x + 2 > 0 \\ x + 1 \leq 3 \end{array}$ 的解集在数轴上表示为（）。

A、 B、 C、 D、

查看试题解析
4. 多边形内角和为 $90 0^{∘}$ ，这个多边形的边数是（）。

A、4 B、5 C、6 D、7

查看试题解析
5. 如下图，BD是△ABC的角平分线， $D E ∥ B C$ ，交AB于E， $∠ A = 6 0^{∘}$ ， $∠ B D C = 9 5^{∘}$ ，则∠BED的度数是（）。

A、 $3 5^{∘}$ B、 $7 0^{∘}$ C、 $11 0^{∘}$ D、 $13 0^{∘}$ A

查看试题解析
6. 若 $x > y$ ，则下列式子错误的是（）

A、 $x + 3 > y + 3$ B、 $x - 6 > y - 6$ C、 $2 y - 5 > 2 x - 5$ D、 $- 3.5 y + 1 > - 3.5 x + 1$

查看试题解析
7. 如下图，已知 $∠ A B C = ∠ D C B$ ，添加以下条件，不能判定 $Δ A B C ≅ Δ D C B$ 的是（）。

A、 $∠ A = ∠ D$ B、 $∠ A C B = ∠ D B C$ C、 $A C = D B$ D、 $A B = D C$

查看试题解析
8. 方程 $5 x + 2 y = - 9$ 与下列方程构成的方程组的解为 ${\begin{array}{l} x = - 2 \\ y = \frac{1}{2} \end{array}$ 的是（）。

A、 $x + 2 y = 1$ B、 $3 x + 2 y = - 8$ C、 $5 x + 4 y = - 3$ D、 $3 x - 4 y = - 8$

查看试题解析
9. 下列说法正确的个数有（）
①三角形的三条高线交于一点。
②三角形的一个外角等于两个内角的和。
③有两边和一角分别相等的两个三角形全等。
④角的内部到角两边距离相等的点，在这个角的平分线上。
⑤各边都相等的多边形一定是正多边形。

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如下图，AD是△ABC的中线，点E是AD的三等分点（点E靠近A点），点F是AD延长线上一点， $E D = D F$ ，连接BE，CF，CE，G是EC的中点，连接BG。有下列说法：

① $C F = B F$ ② $∠ B E C + ∠ E C F = 18 0^{∘}$ ；③△ABD和△ACD的面积相等；④△ECF和△BEC的面积相等；⑤△BGC与△ABD的面积之比是 $1 ： 3$ 。

其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（每小题3分，共18分）

11. 已知方程 $7 x - y = 8$ ，用含x的式子表示y，则y=。

查看试题解析
12. 把“比a的8倍小5的数不小于a的 $\frac{1}{3}$ ”用不等式表示为。

查看试题解析
13. 用一条长18cm的细绳恰好围成一个等腰三角形，其中一边长为4cm，则底边长为cm，

查看试题解析
14. 若关于x的不等式 $3 x - m \leq 0$ 的正整数解为1，2，3，则m的取值范围为。

查看试题解析
15. 已知，AD是△ABC的角平分线，过点D作 $D E ⊥ A C$ ，垂足为点E，作 $D F ⊥ A E$ ，交边AB所在直线于点F，若 $A F = 6 c m ， B F = 2 c m$ ，则AB的长为cm。

查看试题解析
16. 一个长方形的长减少2cm，宽增加1cm，就成为一个正方形，并且正方形的面积比原长方形的面积小 $3 c m^{2}$ ，则原长方形的面积为 $c m^{2}$ 。

查看试题解析

三、解答题（17-18题各6分，19-23题各8分，24-25题各10分，共72分）。

17. 解二元一次方程组：

(1)、 ${\begin{array}{l} x - y = 3 \\ 3 x - 8 y = 14 \end{array}$

(2)、 ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$

查看试题解析
18.

(1)、解一元一次不等式，并在给定数轴上表示解集：
$2 (1 + x) < 3$

(2)、解一元一次不等式组：
${\begin{array}{l} 2 x + 3 \geq x + 11 \\ \frac{2 x + 5}{3} - 1 & < 2 - x \end{array}$

查看试题解析
19. 如图，在 $10 \times 10$ 的网格中的每个小正方形边长都是1，线段交点称作格点。任意连接这些格点，可得到一些线段，请按要求作图。

(1)、请画出△ABC中BC边上的高AD；

(2)、画图中△ABC的一条中线：

(3)、请画出与△ABC只有一个公共边AB且全等的格点三角形（只画一个）；

(4)、直接写出△ABC的面积是。

查看试题解析
20. 如图，在四边形ABCD中， $∠ A = ∠ C = 9 0^{∘}$ ， BE平分∠ABC，DF平分∠ADC，求证：BE//DF。

查看试题解析
21. 如图， $C D ⊥ A B ， B E ⊥ A C$ ，垂足分别为D，E，BE与CD相交于点F， $F B = F C$

(1)、求证： $B D = C E$ ：

(2)、在不添加任何辅助线的前提下，直接写出图中四对全等三角形（注意对应顶点写在对应位置上）。

查看试题解析
22. 萧红中学为了丰富学生的课余生活，计划购买围棋和中国象棋供兴趣班活动使用，若购买3副围棋和5副中国象棋需要98元，若购买8副围棋和3副中国象棋需158元。

(1)、求每副围棋和中国象棋各多少元？

(2)、若决定购买的围棋和中国象棋共40副，总费用不超过550元，那么最多可以购买多少副围棋？

查看试题解析
23. 阅读下列材料，并深入理解“等量代换”的方法：
解答“已知 $x - y = 2$ ，且 $x > 1 ， y < 0$ ，试确定y的取值范围”有如下解法：

解：∵ $x - y = 2$ ∴ $x = y + 2$

∵ $x > 1$ ∴ $y + 2 > 1$ ∴ $y > - 1$ ，

又∵ $y < 0$ ， ∴y的取值范围是 $- 1 < y < 0$ 。

请解答以下问题：

已知，于x，y的方程组 ${\begin{array}{l} 3 x - y = 2 a - 5 \\ x + 2 y = 3 a + 3 \end{array}$ 的解都是正数。

(1)、求a的取值范围；

(2)、若 $a - b = 4$ ，且 $b < 2$ ，求b的取值范围。

查看试题解析
24. 已知，在Rt△ABC中， $∠ B A C = 9 0^{∘}$ ， $A C = A B$ ，点F是射线CA上一点，连接BF，过点C作CE⊥BF，垂足为点E，直线CE，AB相交于点D。

图1 图2 图3

(1)、如图1，当点F在线段CA的延长线上时，求证： $C F = A B + A D$ ；

(2)、如图2，当点F在线段CA上时，求证：EA平分∠DEB；

(3)、如图3，当点F在线段CA上时，若 $C F = \frac{1}{2} C A$ ， △BDE的面积为16，求BE的长。

查看试题解析
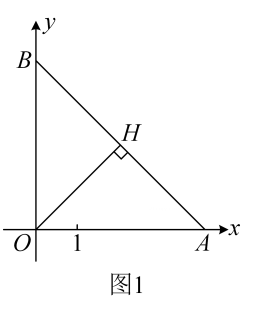
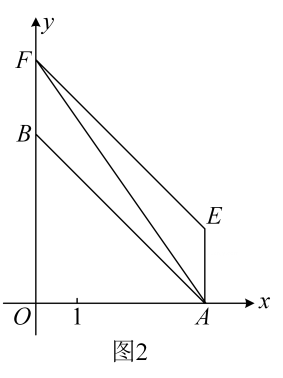
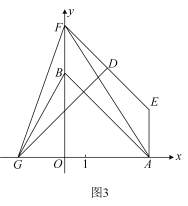25. 已知，在平面直角坐标系中，点O为坐标原点，x轴的正半轴上有点A（4，0），点B（0，b）在y轴正半轴上，且 $∠ O A B = ∠ 0 B A = 4 5^{∘}$

(1)、如图1， $O H ⊥ A B$ 于点H，请直接写出点的坐标：B（，），H（，）；

(2)、如图2，过点A作 $A E ⊥ x$ 轴， $A E = t$ 过点E作EF//AB交y轴于点F，连接AF，设线段OF的长为d，求d与t之间满足的关系式；

(3)、如图3，在（2）的条件下，点D为EF的中点，过点D作DG⊥EF交x轴于点G，连接FG，当 $d = 7$ 时，射线AE上是否存在点P，使得 $B P = B G$ ？若存在，求出满足条件的点P的坐标，若不存在，请说明理由。

查看试题解析