湖北省武汉江岸区2022-2023学年九年级下学期数学5月考试卷
试卷更新日期:2023-06-25 类型:月考试卷
一、 选择题(共10小题,每小题3分,共30分)
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,则-2023的相反数为( )A、-2023 B、2023 C、 D、2. 有4张背面完全相同的卡片,正面分别标有数字2、3、4、5,从中同时抽取两张,则下列事件为随机事件的是( )A、两张卡片的数字之和等于5 B、两张卡片的数字之和等于10 C、两张卡片的数字之和大于或等于2 D、两张卡片的数字之和等于43. 下列小写的希腊字母中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 计算的结果是( )A、 B、 C、 D、5. 如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
4. 计算的结果是( )A、 B、 C、 D、5. 如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( ) A、
A、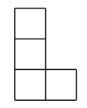 B、
B、 C、
C、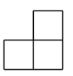 D、
D、 6. 点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数的图象上,则y1、y2、y3 , 的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y27. 若m,n是方程的两根,如图,表示的值所对应的点落在( )
6. 点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数的图象上,则y1、y2、y3 , 的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y27. 若m,n是方程的两根,如图,表示的值所对应的点落在( ) A、第①段 B、第②段 C、第③段 D、第④段8. 小海鸥从家出发,步行到离家a米的公园散步,速度为50米/分钟;6分钟后咩咩也从家出发沿着同一路线骑自行车到公园,咩咩到达公园后立即以原速返回家中,两人离家的距离y(米)与小海鸥出发的时间x(分钟)的函数关系如图所示.小海鸥出发多长时间与咩咩第二次相遇( )
A、第①段 B、第②段 C、第③段 D、第④段8. 小海鸥从家出发,步行到离家a米的公园散步,速度为50米/分钟;6分钟后咩咩也从家出发沿着同一路线骑自行车到公园,咩咩到达公园后立即以原速返回家中,两人离家的距离y(米)与小海鸥出发的时间x(分钟)的函数关系如图所示.小海鸥出发多长时间与咩咩第二次相遇( ) A、9.5 B、9.6 C、9.8 D、109. 如图,△ABC内接于⊙O,若AB= , AC= , BC=7,则⊙O的半径是( )
A、9.5 B、9.6 C、9.8 D、109. 如图,△ABC内接于⊙O,若AB= , AC= , BC=7,则⊙O的半径是( )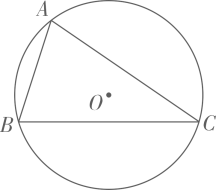 A、 B、 C、 D、10. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3,则方程[x]=x2-2的解有( )个A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、10. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3,则方程[x]=x2-2的解有( )个A、1个 B、2个 C、3个 D、4个二、填空题(共6小题,每小题3分,共18分)
-
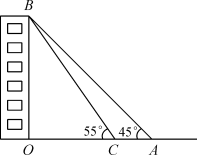
11. 下列各数: , 0,π,中无理数的个数为个.12. 据有关资料显示,长江三峡工程电站的总装机容量是18200000千瓦,请你用科学记数法表示该电站的总装机容量,应记为千瓦.13. 某班准备在甲、乙、丙、丁四位同学中选出两名同学代表班级参加学校举行的“激情五月,唱响青春”为主题的演讲比赛,则乙同学不被选中的概率是.14. 某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B点的仰角为45°,走6米到C处再测得B点的仰角为55°,已知O、A、C在同一条直线上,则新教学楼的高度OB是米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
 15. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
15. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:x
…
-1
0
1
2
…
y=ax2+bx+c
…
m
-1
-1
n
t
…
且当x=-时,与其对应的函数值y>0,有下列结论:①abc>0;②当x>1时,y随x的增大而减小;③关于x的方程ax2+bx+c=t的两个根是和1-;④m+n> . 其中正确的结论是 . (填写序号)
16. 如图,点D、E、F、G分别在锐角ΔABC的边上,四边形DEGF为矩形,DE=2DF, , BF+CG= , 则.
三、解答题(共8小题,共72分)
-
17. 解不等式组 , 请按下列步骤完成解答:

(I)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)将不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为 ▲ .
18. 如图, , , . (1)、求的度数;(2)、若平分 , 求的度数.19. 为了解本校九年级学生的体质健康情况,朱老师随机抽取32名学生进行了一次体质健康测试,规定分数在75分(包含75分)以上为良好;根据测试成绩制成统计图表.
(1)、求的度数;(2)、若平分 , 求的度数.19. 为了解本校九年级学生的体质健康情况,朱老师随机抽取32名学生进行了一次体质健康测试,规定分数在75分(包含75分)以上为良好;根据测试成绩制成统计图表.
组别
分数段
人数
A
x<60
2
B
60≤x<75
5
C
75≤x<90
a
D
x≥90
12
请根据上述信息解答下列问题:
(1)、本次调查中的样本容量是 , a=;(2)、补全条形统计图;样本数据的中位数位于 组;(3)、该校九年级学生有960人,估计该校九年级学生体质健康测试成绩为良好的有多少人?20. 如图,AB是圆O的直径,C为圆上的一点,D为弧BC的中点,连接BC,AD,过点C作AD的垂线交AB于点E. (1)、求证:AC=AE;(2)、AB=5,AD=4,求AE的长.21. 如图是由小正方形组成的7×7网格,每个小正方形的顶点叫做格点.A、B、C三点是格点,仅用无刻度的直尺在给定网格中完成画图并保留作图痕迹.
(1)、求证:AC=AE;(2)、AB=5,AD=4,求AE的长.21. 如图是由小正方形组成的7×7网格,每个小正方形的顶点叫做格点.A、B、C三点是格点,仅用无刻度的直尺在给定网格中完成画图并保留作图痕迹.
图(1) 图(2)
(1)、在图(1)中,点D为线段AB与网格线的交点,在线段AC上画点E,使线段DE与线段BC平行,再在线段AB上画点P,使tan∠ACP=;(2)、在图(2)中,点F为线段AB与网格线的交点,在图中画出两格点G1 , G2 , 使FG1=FG2=BC.O为线段AC与网格线的交点,以O为位似中心,把线段AF扩大为原来的2倍,画出对应线段A′F′.22. 作为武汉市菜篮子工程生产基地,我市新洲区光明村白菜丰收却面临滞销的情况,在武汉市政府的关心和帮助下,各地的订单如雪片般“飞”向光明村,千亩白菜的滞销状况得到较大改善.市政府拟采用水陆联运的方式,派出车队到田间将白菜装车后运往码头再装船销往各地,负责人统计了解装载情况,发现运送到码头的白菜量y(单位:吨)随时间x(单位:小时)的变化情况如图2所示,当0≤x≤10时,y是x的二次函数,图象经过A(0,100),顶点B(10,600);当10<x≤12时,累计数量保持不变.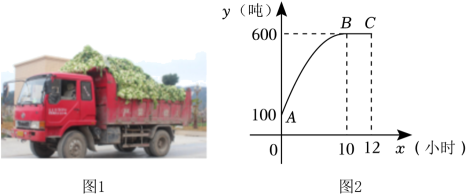 (1)、求y与x之间的函数解析式;(2)、在码头安装了2台传送设备,在运送白菜的同时,可将码头上的白菜直接传送到船上,大大提高了工作效率.每台传送设备每小时可传送20吨白菜到船上.码头上等待传送上船的白菜最多时有多少吨?全部白菜都传送完成需要多少时间?23. 问题背景:
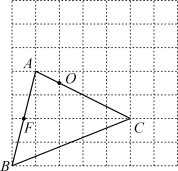
(1)、求y与x之间的函数解析式;(2)、在码头安装了2台传送设备,在运送白菜的同时,可将码头上的白菜直接传送到船上,大大提高了工作效率.每台传送设备每小时可传送20吨白菜到船上.码头上等待传送上船的白菜最多时有多少吨?全部白菜都传送完成需要多少时间?23. 问题背景: (1)、如图1,正方形ABCD,点E、F分别在边AB、BC上,连接AF与DE交于点O,有∠FOD=90°,则= , 若E为AB中点,则;(2)、尝试应用:
(1)、如图1,正方形ABCD,点E、F分别在边AB、BC上,连接AF与DE交于点O,有∠FOD=90°,则= , 若E为AB中点,则;(2)、尝试应用:如图2,平行四边形ABCD,AB=5,BC=4,点E边AB上,点F在边BC的延长线上,连接AF与DE交于点O,当∠FOD=∠B时,求的值;
(3)、类比拓展:如图3,菱形ABCD中,(m>2),点E在边AB上,点F是BC延长线上一点,且满足 , 连接AF与DE交于点O时,∠DAO=∠AED;直接写出cos∠ABF的值.(用含m的式子表示)
24. 如图1,抛物线:y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(-3,0),C(0,3)两点,交x轴于另一点B.
 (1)、求抛物线的解析式;(2)、P在直线AC上方抛物线上,作PD//y轴,交线段AC于点D,作PE//x轴,交抛物线于另一点E,若2PD=PE,求点P的坐标;(3)、如图2,将抛物线平移至顶点在原点,直线PQ分别与x,y轴交于E,F两点,与新抛物线交于P、Q两点,做PQ的垂直平分线MN交y轴于点N,若PQ=2MN,求证:=4OE.
(1)、求抛物线的解析式;(2)、P在直线AC上方抛物线上,作PD//y轴,交线段AC于点D,作PE//x轴,交抛物线于另一点E,若2PD=PE,求点P的坐标;(3)、如图2,将抛物线平移至顶点在原点,直线PQ分别与x,y轴交于E,F两点,与新抛物线交于P、Q两点,做PQ的垂直平分线MN交y轴于点N,若PQ=2MN,求证:=4OE.