广东省揭阳市惠来县2022-2023学年八年级下册期中考试数学试卷
试卷更新日期:2023-06-25 类型:期中考试
一、选择题(共10小题,满分30分,每小题3分)
-
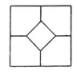
1. 下列图形是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、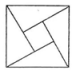 C、
C、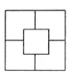 D、
D、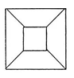 2. 在直角坐标系中,点向右平移4个单位长度后的坐标为( )A、(-6,3) B、(2,3) C、(-2,-1) D、(-2,7)3. 是不大于5的数,则下列表示正确的是( )A、 B、 C、 D、4. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、5. 如图,在平面直角坐标系中,一次函数经过A,B两点,若点B的坐标为(3,0),则不等式的解集是( )
2. 在直角坐标系中,点向右平移4个单位长度后的坐标为( )A、(-6,3) B、(2,3) C、(-2,-1) D、(-2,7)3. 是不大于5的数,则下列表示正确的是( )A、 B、 C、 D、4. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、5. 如图,在平面直角坐标系中,一次函数经过A,B两点,若点B的坐标为(3,0),则不等式的解集是( ) A、 B、 C、 D、6. 不等式 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、6. 不等式 的解集在数轴上表示正确的是( )A、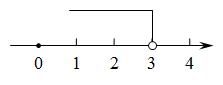 B、
B、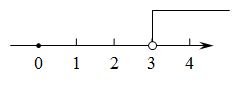 C、
C、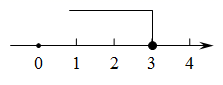 D、
D、 7. 不等式的正整数解有( )A、1个 B、2个 C、3个 D、4个8. 如图,在中,AD平分 , 若 , , 则( )
7. 不等式的正整数解有( )A、1个 B、2个 C、3个 D、4个8. 如图,在中,AD平分 , 若 , , 则( )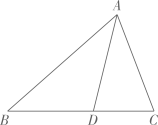 A、25:16 B、5:4 C、16:25 D、4:59. 在三角形ABC中, , DE垂直平分斜边AB,分别交AB,BC于D,E.若 , 求( )
A、25:16 B、5:4 C、16:25 D、4:59. 在三角形ABC中, , DE垂直平分斜边AB,分别交AB,BC于D,E.若 , 求( ) A、120° B、130° C、140° D、150°10. 为了美化校园,学校决定利用现有的2660盆甲种花卉和盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉盆,搭配一个B种造型需甲种花卉40盆,乙种花卉盆.设搭配A种造型x个,你认为下列符合题意的不等式组是( )A、 B、 C、 D、
A、120° B、130° C、140° D、150°10. 为了美化校园,学校决定利用现有的2660盆甲种花卉和盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉盆,搭配一个B种造型需甲种花卉40盆,乙种花卉盆.设搭配A种造型x个,你认为下列符合题意的不等式组是( )A、 B、 C、 D、二、填空题(共5小题,满分15分,每小题3分)
-
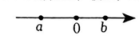
11. 已知 , 是有理数,它们在数轴上的对应点的位置如图所示,把 , , , 按照从小到大的顺序排列,用不等式可表示为.
 12. 如图,一个含有30°角的三角板ABC,绕点B顺时针旋转到的位置,使A,B,在同一条直线上,则旋转角的度数为.
12. 如图,一个含有30°角的三角板ABC,绕点B顺时针旋转到的位置,使A,B,在同一条直线上,则旋转角的度数为.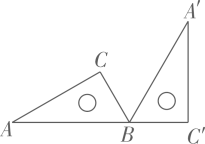 13. 命题“若 , 则”的逆命题是.14. 一个直角三角形的两边长分别为1和2,则第三边长为.15. 若关于x的不等式组有且仅有一个整数解 , 则实数a的取值范围是.
13. 命题“若 , 则”的逆命题是.14. 一个直角三角形的两边长分别为1和2,则第三边长为.15. 若关于x的不等式组有且仅有一个整数解 , 则实数a的取值范围是.三、解答题(一)(本大题3小题,每小题8分,共24分)
-
16. 解下列不等式(1)、;(2)、17. 解不等式组 , 请按下列步骤完成解答:(1)、解不等式①,得.(2)、解不等式②,得.(3)、原不等式组的解集为.18. 如图,在平面直角坐标系中,的三个顶点坐标分别是 , , , 将绕点A逆时针旋转90°得到.
 (1)、画出 , 写出点 , 的坐标;(2)、请直接写出线段与轴交点的坐标.
(1)、画出 , 写出点 , 的坐标;(2)、请直接写出线段与轴交点的坐标.四、解答题(二)(本大题3小题,每小题9分,共27分)
-
19. 如图中,点D在AB上,已知.
 (1)、求的大小;(2)、若 , , 求的周长.20. 我校举行数学竞赛,一共有25道题,满分100分,每答对一题得4分,答错扣一分,不答记0分。(1)、某同学只有一道题未作答,最后得分86分,则该生一共答对多少题?(2)、若规定参赛者每题必须作答,得分大于或等于90分,才可以评为一等奖,则参赛者至少答对多少题才能获评一等奖?21. 如图,已知直线经过点 , , 与直线交于C点、
(1)、求的大小;(2)、若 , , 求的周长.20. 我校举行数学竞赛,一共有25道题,满分100分,每答对一题得4分,答错扣一分,不答记0分。(1)、某同学只有一道题未作答,最后得分86分,则该生一共答对多少题?(2)、若规定参赛者每题必须作答,得分大于或等于90分,才可以评为一等奖,则参赛者至少答对多少题才能获评一等奖?21. 如图,已知直线经过点 , , 与直线交于C点、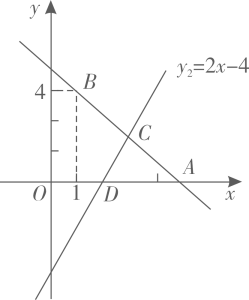 (1)、求直线的解析式以及以与x轴的交点D的坐标;(2)、求C点的坐标;(3)、根据图象,直接写出关于的不等式时x的取值范围.
(1)、求直线的解析式以及以与x轴的交点D的坐标;(2)、求C点的坐标;(3)、根据图象,直接写出关于的不等式时x的取值范围.五、解答题(三)(本大题2小题,每小题12分,共24分)
-
22. 如图,在等边中, , 点M以2cm/s的速度从点B出发向点A运动(不与点A重合),点N以3cm/s的速度从点C出发向点B运动(不与点B重合),设点M,N同时运动,运动时间为.
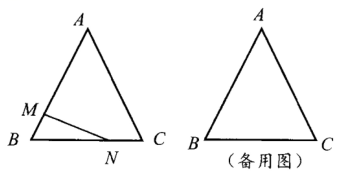 (1)、在点M,N运动过程中,经过几秒时为等边三角形?(2)、在点M,N运动过程中,的形状能否为直角三角形,若能,请计算运动时间;若不能,请说明理由.23. 先阅读理解下面的例题,再按要求解答下列问题:
(1)、在点M,N运动过程中,经过几秒时为等边三角形?(2)、在点M,N运动过程中,的形状能否为直角三角形,若能,请计算运动时间;若不能,请说明理由.23. 先阅读理解下面的例题,再按要求解答下列问题:例题:解一元二次不等式.
解∵ , ∴ , 可化为.
由有理数的乘法法则:两数相乘,同号得正,得:① , ②
解不等式组①,得 , 解不等式组②,得 ,
∴的解集为或
即一元二次不等式的解集为x>2或.
(1)、一元二次不等式的解集为;(2)、试解一元二次不等式;(3)、试解不等式.