江苏省扬州市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将该选项的字母代号填涂在答题卡相应位置上)
-
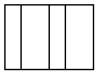
1. -3的绝对值是( )A、3 B、 C、 D、2. 若 , 则括号内应填的单项式是( )A、a B、 C、 D、3. 空气的成分(除去水汽、杂质等)是:氮气约占78%,氧气约占21%,其他微量气体约占1%.要反映上述信息,宜采用的统计图是( )A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图4. 下列图形中是棱锥的侧面展开图的是( )A、
 B、
B、 C、
C、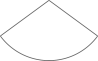 D、
D、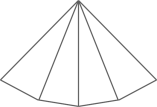 5. 已知 , 则a、b、c的大小关系是( )A、 B、 C、 D、6. 函数的大致图像是( )A、
5. 已知 , 则a、b、c的大小关系是( )A、 B、 C、 D、6. 函数的大致图像是( )A、 B、
B、 C、
C、 D、
D、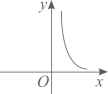 7. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、88. 已知二次函数(a为常数,且),下列结论:
7. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、88. 已知二次函数(a为常数,且),下列结论:①函数图象一定经过第一、二、四象限;②函数图象一定不经过第三象限;③当时,y随x的增大而减小;④当时,y随x的增大而增大.
其中所有正确结论的序号是( )A、①② B、②③ C、② D、③④二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
-
9. 扬州市大力推进城市绿化发展,2022年新增城市绿地面积约2345000平方米,数据2345000用科学记数法表示为 .10. 分解因式: .11. 如果一个多边形每一个外角都是 , 那么这个多边形的边数为 .12. 某种绿豆在相同条件下发芽试验的结果如下:
每批粒数n
2
5
10
50
100
500
1000
1500
2000
3000
发芽的频数m
2
4
9
44
92
463
928
1396
1866
2794
发芽的频率(精确到0.001)
1.000
0.800
0.900
0.880
0.920
0.926
0.928
0.931
0.933
0.931
这种绿豆发芽的概率的估计值为(精确到0.01).
13. 关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 .14. 用半径为 , 面积为的扇形纸片,围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .15. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .16. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若 , 则每个直角三角形的面积为 .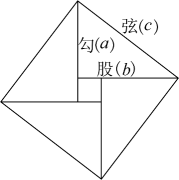 17. 如图,中, , 以点B为圆心,适当长为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点E,作射线交于点D,则线段的长为 .
17. 如图,中, , 以点B为圆心,适当长为半径画弧,分别交于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点E,作射线交于点D,则线段的长为 . 18. 如图,已知正方形的边长为1,点E、F分别在边上,将正方形沿着翻折,点B恰好落在边上的点处,如果四边形与四边形的面积比为3∶5,那么线段的长为 .
18. 如图,已知正方形的边长为1,点E、F分别在边上,将正方形沿着翻折,点B恰好落在边上的点处,如果四边形与四边形的面积比为3∶5,那么线段的长为 .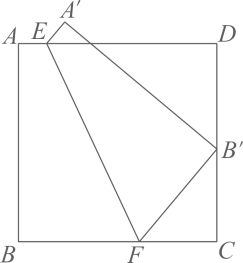
三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
-
19. 计算:(1)、;(2)、 .20. 解不等式组并把它的解集在数轴上表示出来.21. 某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
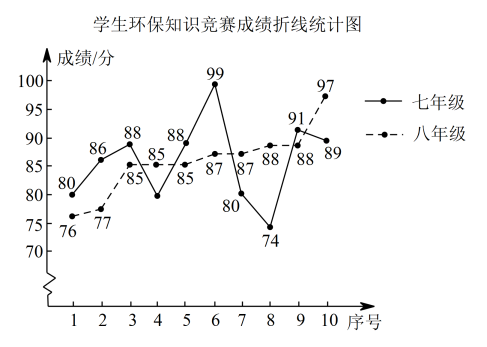
平均数
众数
中位数
七年级参赛学生成绩
85.5
m
87
八年级参赛学生成绩
85.5
85
n
根据以上信息,回答下列问题:
(1)、填空: , ;(2)、七、八年级参赛学生成绩的方差分别记为、 , 请判断(填“”“”或“”);(3)、从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.22. 扬州是个好地方,有着丰富的旅游资源.某天甲、乙两人来扬州旅游,两人分别从 , , 三个景点中随机选择一个景点游览.(1)、甲选择景点的概率为;(2)、请用画树状图或列表的方法,求甲、乙两人中至少有一人选择景点的概率.23. 甲、乙两名学生到离校的“人民公园”参加志愿者活动,甲同学步行,乙同学骑自行车,骑自行车速度是步行速度的4倍,甲出发后乙同学出发,两名同学同时到达,求乙同学骑自行车的速度.24. 如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.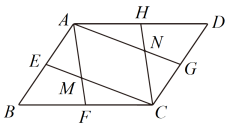 (1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.25. 如图,在中, , 点D是上一点,且 , 点O在上,以点O为圆心的圆经过C、D两点.
(1)、求证:四边形是平行四边形;(2)、若的面积为4,求的面积.25. 如图,在中, , 点D是上一点,且 , 点O在上,以点O为圆心的圆经过C、D两点.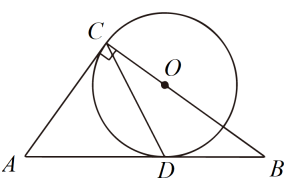 (1)、试判断直线与的位置关系,并说明理由;(2)、若的半径为3,求的长.26. 近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2920元,甲种头盔的单价比乙种头盔的单价高11元.(1)、甲、乙两种头盔的单价各是多少元?(2)、商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,使此次购买头盔的总费用最小?最小费用是多少元?27. 【问题情境】
(1)、试判断直线与的位置关系,并说明理由;(2)、若的半径为3,求的长.26. 近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2920元,甲种头盔的单价比乙种头盔的单价高11元.(1)、甲、乙两种头盔的单价各是多少元?(2)、商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,使此次购买头盔的总费用最小?最小费用是多少元?27. 【问题情境】在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动,两块三角板分别记作和 , 设 .
【操作探究】
如图1,先将和的边、重合,再将绕着点A按顺时针方向旋转,旋转角为 , 旋转过程中保持不动,连接 .
 (1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .28. 在平面直角坐标系中,已知点A在y轴正半轴上.
(1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .28. 在平面直角坐标系中,已知点A在y轴正半轴上. (1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.
(1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.① ▲ ;
②如图1,已知菱形的顶点B、C、D在该二次函数的图象上,且轴,求菱形的边长;
③如图2,已知正方形的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究是否为定值.如果是,求出这个值;如果不是,请说明理由.
(2)、已知正方形的顶点B、D在二次函数(a为常数,且)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.