江苏省苏州市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用rId8铅笔涂在答题卡相对应的位置上.
-
1. 有理数的相反数是( )A、 B、 C、 D、2. 古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )A、
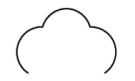 B、
B、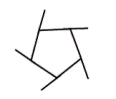 C、
C、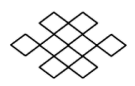 D、
D、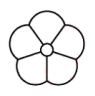 3. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( )
3. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( ) A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则4. 今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则4. 今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( ) A、长方体 B、正方体 C、圆柱 D、三棱锥5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,转盘中四个扇形的面积都相等,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( )
A、长方体 B、正方体 C、圆柱 D、三棱锥5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,转盘中四个扇形的面积都相等,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( )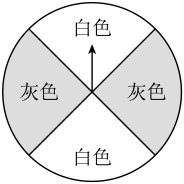 A、 B、 C、 D、7. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )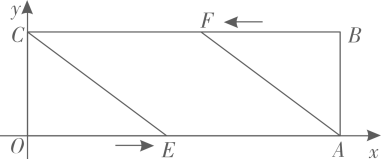 A、 B、 C、 D、8. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )
A、 B、 C、 D、8. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )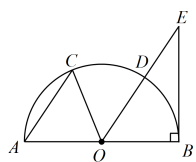 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相对应的位置上.
-
9. 使 有意义的x的取值范围是 .
10. 因式分解:a2+ab= .
11. 分式方程的解为 .12. 在比例尺为的地图上,量得两地在地图上的距离为厘米,即实际距离为28000000厘米.数据28000000用科学记数法可表示为 .13. 小惠同学根据某市统计局发布的2023年第一季度高新技术产业产值数据,绘制了如图所示的扇形统计图,则“新材料”所对应扇形的圆心角度数是 .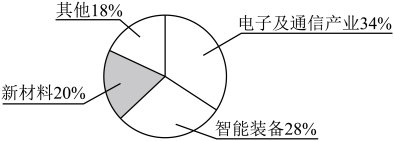 14. 已知一次函数的图象经过点和 , 则 .15. 如图,在中, , 垂足为 . 以点为圆心,长为半径画弧,与分别交于点 . 若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为 , 则 . (结果保留根号)
14. 已知一次函数的图象经过点和 , 则 .15. 如图,在中, , 垂足为 . 以点为圆心,长为半径画弧,与分别交于点 . 若用扇形围成一个圆锥的侧面,记这个圆锥底面圆的半径为;用扇形围成另一个圆锥的侧面,记这个圆锥底面圆的半径为 , 则 . (结果保留根号)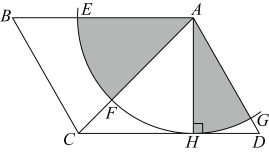 16. 如图, . 过点作 , 延长到 , 使 , 连接 . 若 , 则 . (结果保留根号)
16. 如图, . 过点作 , 延长到 , 使 , 连接 . 若 , 则 . (结果保留根号)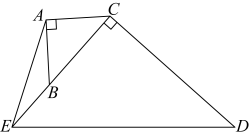
三、解答题:本大题共11小题,共82分.把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.
-
17. 计算: .18. 解不等式组:19. 先化简,再求值: , 其中 .20. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .
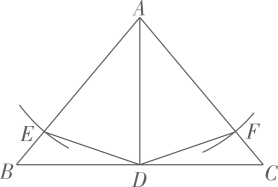 (1)、求证:;(2)、若 , 求的度数.21. 一只不透明的袋子中装有4个小球,分别标有编号 , 这些小球除编号外都相同.(1)、搅匀后从中任意摸出1个球,这个球的编号是2的概率为 .(2)、搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大1的概率是多少?(用画树状图或列表的方法说明)22. 某初中学校为加强劳动教育,开设了劳动技能培训课程.为了解培训效果,学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测,两次检测项目相同,评委依据同一标准进行现场评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分(比如,某同学检测等级为“优秀”,即得8分).学校随机抽取32名学生的2次检测等级作为样本,绘制成下面的条形统计图:
(1)、求证:;(2)、若 , 求的度数.21. 一只不透明的袋子中装有4个小球,分别标有编号 , 这些小球除编号外都相同.(1)、搅匀后从中任意摸出1个球,这个球的编号是2的概率为 .(2)、搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大1的概率是多少?(用画树状图或列表的方法说明)22. 某初中学校为加强劳动教育,开设了劳动技能培训课程.为了解培训效果,学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测,两次检测项目相同,评委依据同一标准进行现场评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分(比如,某同学检测等级为“优秀”,即得8分).学校随机抽取32名学生的2次检测等级作为样本,绘制成下面的条形统计图: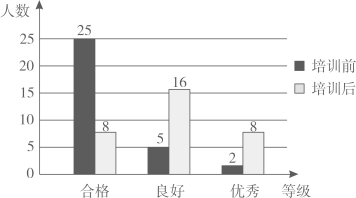 (1)、这32名学生在培训前得分的中位数对应等级应为;(填“合格”、“良好”或“优秀”)(2)、求这32名学生培训后比培训前的平均分提高了多少?(3)、利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少?23. 四边形不具有稳定性,工程上可利用这一性质解决问题.如图是某篮球架的侧面示意图,为长度固定的支架,支架在处与立柱连接(垂直于 , 垂足为),在处与篮板连接(所在直线垂直于),是可以调节长度的伸缩臂(旋转点处的螺栓改变的长度,使得支架绕点旋转,从而改变四边形的形状,以此调节篮板的高度).已知 , 测得时,点离地面的高度为 . 调节伸缩臂 , 将由调节为 , 判断点离地面的高度升高还是降低了?升高(或降低)了多少?(参考数据:)
(1)、这32名学生在培训前得分的中位数对应等级应为;(填“合格”、“良好”或“优秀”)(2)、求这32名学生培训后比培训前的平均分提高了多少?(3)、利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少?23. 四边形不具有稳定性,工程上可利用这一性质解决问题.如图是某篮球架的侧面示意图,为长度固定的支架,支架在处与立柱连接(垂直于 , 垂足为),在处与篮板连接(所在直线垂直于),是可以调节长度的伸缩臂(旋转点处的螺栓改变的长度,使得支架绕点旋转,从而改变四边形的形状,以此调节篮板的高度).已知 , 测得时,点离地面的高度为 . 调节伸缩臂 , 将由调节为 , 判断点离地面的高度升高还是降低了?升高(或降低)了多少?(参考数据:) 24. 如图,一次函数的图象与反比例函数的图象交于点 . 将点沿轴正方向平移个单位长度得到点为轴正半轴上的点,点的横坐标大于点的横坐标,连接的中点在反比例函数的图象上.
24. 如图,一次函数的图象与反比例函数的图象交于点 . 将点沿轴正方向平移个单位长度得到点为轴正半轴上的点,点的横坐标大于点的横坐标,连接的中点在反比例函数的图象上.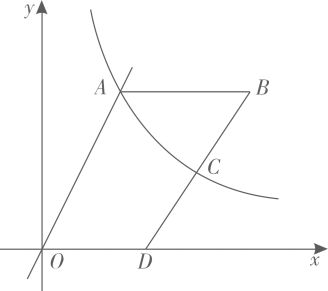 (1)、求的值;(2)、当为何值时,的值最大?最大值是多少?25. 如图,是的内接三角形,是的直径, , 点在上,连接并延长,交于点 , 连接 , 作 , 垂足为 .
(1)、求的值;(2)、当为何值时,的值最大?最大值是多少?25. 如图,是的内接三角形,是的直径, , 点在上,连接并延长,交于点 , 连接 , 作 , 垂足为 .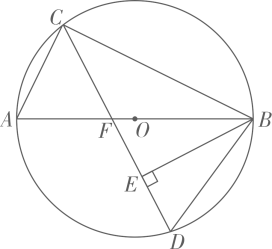 (1)、求证:;(2)、若 , 求的长.26. 某动力科学研究院实验基地内装有一段笔直的轨道 , 长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为 , 滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿 , 然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为 , 右端离点的距离为 , 记与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数;滑块从点出发到最后返回点 , 整个过程总用时(含停顿时间).请你根据所给条件解决下列问题:
(1)、求证:;(2)、若 , 求的长.26. 某动力科学研究院实验基地内装有一段笔直的轨道 , 长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为 , 滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿 , 然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为 , 右端离点的距离为 , 记与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数;滑块从点出发到最后返回点 , 整个过程总用时(含停顿时间).请你根据所给条件解决下列问题: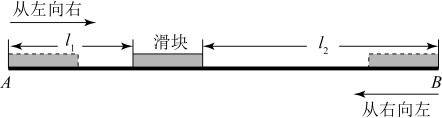 (1)、滑块从点到点的滑动过程中,的值;(填“由负到正”或“由正到负”)(2)、滑块从点到点的滑动过程中,求与的函数表达式;(3)、在整个往返过程中,若 , 求的值.27. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .
(1)、滑块从点到点的滑动过程中,的值;(填“由负到正”或“由正到负”)(2)、滑块从点到点的滑动过程中,求与的函数表达式;(3)、在整个往返过程中,若 , 求的值.27. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .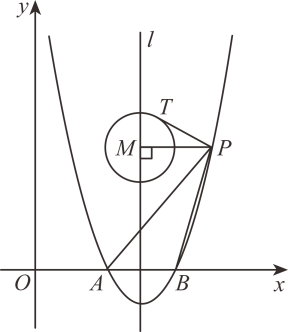 (1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.
(1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.