江苏省盐城市滨海县一中教育集团2022-2023学年下学期第二次阶段调研七年级数学试题

试卷更新日期：2023-06-25 类型：月考试卷

进入出卷网下载

一、选择题.（本大题共8题，共24分）

1. 计算a⁶÷a²的结果是（）

A、a² B、a³ C、a⁴ D、a⁶

查看试题解析
2. 下列方程中：①2x+y＝4；②3xy＝7；③x²+2y＝0；④ $\frac{1}{x} -$ 2＝y；⑤2x+y+z＝1，二元一次方程的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 二元一次方程2x+3y＝8正整数解的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 已知a＞b，则下列不等关系中正确的是（）

A、ac＞bc B、a＋c＞b＋c C、a－1＞b＋1 D、ac²＞bc²

查看试题解析
5.
如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数等于（）
　

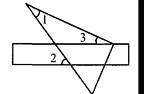A、20° B、50° C、30° D、15°

查看试题解析
6. 如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）

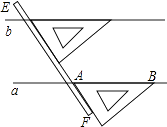A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
7. 《九章算术》中有这样的问题：只闻隔壁人分银，不知多少银和人；每人6两少6两，每人半斤多半斤；试问各位善算者，多少人分多少银注：这里的斤是指市斤，1市斤等于10两，设共有x人，y两银子，下列方程组中正确的是（）

A、 ${\begin{cases} 6 x + 6 = y \\ 5 x - 5 = y \end{cases}$ B、 ${\begin{cases} 6 x + 6 = y \\ 5 x + 5 = y \end{cases}$ C、 ${\begin{cases} 6 x - 6 = y \\ 5 x - 5 = y \end{cases}$ D、 ${\begin{cases} 6 x - 6 = y \\ 5 x + 5 = y \end{cases}$

查看试题解析
8. 关于x的不等式x－a≥1.若x＝1是不等式的解，x＝－1不是不等式的解，则a的范围为（）

A、－2≤a≤0 B、－2＜a＜0 C、－2≤a＜0 D、－2＜a≤0

查看试题解析

二、填空题.（本大题共10题，共30分）

9. 将0.0000036用科学记数法表示为.

查看试题解析
10. 若 $a^{m}$ =4， $a^{n}$ =8，则 ${a^{m}}^{+ n}$ =.

查看试题解析
11. 一个n边形的内角和为1080°，则n= ．

查看试题解析
12. 已知三角形两边的长分别为1、5，第三边长为整数，则第三边的长为．

查看试题解析
13. （a-2）x^|^a^|-1+3y＝1是关于x、y的二元一次方程，则a＝.

查看试题解析
14. 已知 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是方程2x-ay＝3的一个解，则a=.

查看试题解析
15. 若实数m，n满足 $| m - n - 5 | + {(2 m + n - 4)}^{2} = 0$ ，则 $3 m + n =$ ．

查看试题解析
16. 已知关于x的方程3x+2（3a+1）＝6x+a的解为非负数，则a的范围为．

查看试题解析
17. 已知不等式组 ${\begin{array}{l} x < 1 \\ x > n \end{array}$ 有3个整数解，则n的取值范围是.

查看试题解析
18. 如图，按下面的程序进行运算．规定：程序运行到“判断结果是否大于28”为一次运算．若运算进行了3次才停止，则x的取值范围是.

查看试题解析

三、解答题.（本大题共9题，共96分）

19. 解下列方程组.

(1)、 ${\begin{cases} x - y = 2 \\ 2 x + y = 7 \end{cases}$

(2)、 ${\begin{cases} x - 2 y = 3 \\ \frac{1}{2} x + \frac{3}{4} y = \frac{13}{4} \end{cases}$

查看试题解析
20. 解下列不等式，并把解集在数轴上表示出来.

(1)、 $5 x - 4 \leq 2 + 7 x$

(2)、 $\frac{x - 1}{3} > \frac{x}{2} - 1$

查看试题解析
21. 解不等式组 ${\begin{cases} 3 x - 5 \geq 2 (x - 2 ） \\ \frac{x}{2} \geq x - 2 \end{cases}$ ，并写出它的所有整数解.

查看试题解析
22. 当x取何正整数时，代数式 $\frac{x + 1}{3} - \frac{2 x - 1}{4}$ 的值不小于代数式 $\frac{x - 3}{6}$ 的值？

查看试题解析
23. 小红和小风两人在解关于x，y的方程组 ${\begin{cases} a x + 3 y = 5 \\ b x + 2 y = 8 \end{cases}$ 时，小红只因看错了系数a，得到方程组的解为 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$ ，小风只因看错了系数b，得到方程组的解为 ${\begin{cases} x = 1 \\ y = 4 \end{cases}$ .

(1)、求a、b的值；

(2)、求原方程组的解．

查看试题解析
24. 已知关于x，y的二元一次方程组 ${\begin{cases} 2 x + y = 1 + 2 m \\ x + 2 y = 2 - m \end{cases}$ 的解满足不等式x+y>0.

(1)、求实数m的取值范围．

(2)、在⑴的条件下，若不等式（2m+1）x-2m＜1的解为x＞1，请写出整数m的值．

查看试题解析
25. 小李家装修，客厅共需某种型号的地砖100块，经市场调查发现，如果购买彩色地砖40块和单色地砖60块则共需花费5600元，如果购买彩色地砖和单色地砖各50块，则需花费6000元．

(1)、求两种型号的地砖的单价各是多少元？

(2)、如果厨房也要铺设这两种型号的地砖共60块，且购买地砖的费用不超过3400元，那么彩色地砖最多能采购多少块？

查看试题解析
26. 已知关于x，y的方程组 ${\begin{array}{l} n x + (n + 1) y = n + 2 \\ x - 2 y + m x = - 5 \end{array}$ (n是常数)．

(1)、当n=1时，则方程组可化为 ${\begin{array}{l} x + 2 y = 3 \\ x - 2 y + m x = - 5 \end{array}$
①请直接写出方程x+2y=3的所有非负整数解．
②若该方程组的解也满足方程x+y=2，求m的值．

(2)、当n=3时，如果方程组有整数解，求整数m的值．

查看试题解析
27.

(1)、【阅读感悟】
小明的数学研学作业单上有这样一道题：已知 $- x + y = 2$ ，且 $x < 3$ ， $y \geq 0$ ，设 $w = x + y - 2$ ，那么w的取值范围是什么？

小明回顾做过的一道简单的类似题目：已知： $- 1 < x < 2$ ，设y= $x + 1$ ，那么y的取值范围是.（请你直接写出答案）

(2)、【初步探究】

小明想：可以将研学单上的复杂问题转化为上面回顾的类似题目.

由 $- x + y = 2$ 得 $y = 2 + x$ ，则 $w = x + y - 2 = x + 2 + x - 2 = 2 x$ ，

由 $x < 3$ ， $y \geq 0$ ，得关于x的一元一次不等式组，

解该不等式组得到x的取值范围为，

则w的取值范围是 .

(3)、【问题解决】
已知a-b＝4，且a＞1，b＜2，设t=a+b，求t的取值范围；

(4)、已知a-b＝n（n是大于0的常数），且a＞1，b≤1， $2 a + b$ 的最大值为.（用含n的代数式表示）；

(5)、【拓展应用】

若 $3 x = 6 y + 12 = 2 z$ ，且 $x > 0$ ， $y \geq - 4$ ， $z \leq 9$ ，设 $m = 2 x - 2 y - z$ ，且m为整数，那么m所有可能的值的和为 .

查看试题解析