贵州省铜仁市万山区2023年中考一模数学试题
试卷更新日期:2023-06-25 类型:中考模拟
一、单选题
-
1. 在实数 , , , 中,有理数是( )A、 B、 C、 D、2. 2022年4月18日,国家统计局发布数据,今年一季度国内生产总值270178亿元.同比增长4.8%,比2021年四季度环比增长1.3%.把27017800000000用科学记数法表示为( )A、 B、 C、 D、3. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下表是2022年1月—5月遵义市PM2.5(空气中直径小于等于2.5微米的颗粒)的平均值,这组数据的众数是( )
4. 下表是2022年1月—5月遵义市PM2.5(空气中直径小于等于2.5微米的颗粒)的平均值,这组数据的众数是( )月份
1月
2月
3月
4月
5月
PM2.5(单位:mg/m3)
24
23
24
25
22
A、22 B、23 C、24 D、255. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 如图,直线 ,直线c与直线a,b分别相交于点A,B, ,垂足为C.若 ,则 ( ) A、52° B、45° C、38° D、26°7. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、8. 在一个不透明的布袋内,有红球5个,黄球4个,白球1个,蓝球3个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,则摸中哪种球的概率最大( )A、红球 B、黄球 C、白球 D、蓝球9. 如图,在中,是边上的点, , , 则与的周长比是( )
A、52° B、45° C、38° D、26°7. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、8. 在一个不透明的布袋内,有红球5个,黄球4个,白球1个,蓝球3个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,则摸中哪种球的概率最大( )A、红球 B、黄球 C、白球 D、蓝球9. 如图,在中,是边上的点, , , 则与的周长比是( ) A、 B、 C、 D、10. 如图,是的两条半径,点C在上,若 , 则的度数为( )
A、 B、 C、 D、10. 如图,是的两条半径,点C在上,若 , 则的度数为( ) A、 B、 C、 D、11. 下列计算错误的是( )A、 B、 C、 D、12. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论:
A、 B、 C、 D、11. 下列计算错误的是( )A、 B、 C、 D、12. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: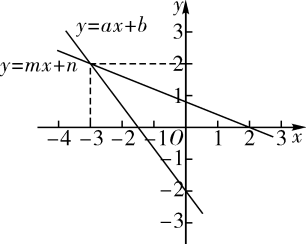
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
13. 把多项式 因式分解,结果为.14. 在一个不透明的袋中装有除颜色外其余都相同的5个小球,其中3个红球、2个黄球.如果第一次先从袋中摸出1个球后不放回,第二次再从袋中摸出1个球,那么两次都摸到黄球的概率是 .15. 不等式组的解集是.16. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.

三、解答题
-
17. 在平面直角坐标系内有三点A(−1,4)、B(−3,2)、C(0,6).(1)、求过其中两点的直线的函数表达式(选一种情形作答);(2)、判断A、B、C三点是否在同一直线上,并说明理由.18. 小星想了解全国2019年至2021年货物进出口总额变化情况,他根据国家统计局2022发布的相关信息,绘制了如下的统计图,请利用统计图中提供的信息回答下列问题:
 (1)、为了更好的表现出货物进出口额的变化趋势,你认为应选择统计图更好(填“条形”或“折线”);(2)、货物进出口差额是衡量国家经济的重要指标,货物出口总额超过货物进口总额的差额称为货物进出口顺差,2021年我国货物进出口顺差是万亿元;(3)、写出一条关于我国货物进出口总额变化趋势的信息.19. 科学规范戴口罩是阻断新冠病毒传播的有效措施之一,某口罩生产厂家接到一公司的订单,生产一段时间后,还剩280万个口罩未生产,厂家因更换设备,生产效率比更换设备前提高了40%.结果刚好提前2天完成订单任务.求该厂家更换设备前和更换设备后每天各生产多少万个口罩?20. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
(1)、为了更好的表现出货物进出口额的变化趋势,你认为应选择统计图更好(填“条形”或“折线”);(2)、货物进出口差额是衡量国家经济的重要指标,货物出口总额超过货物进口总额的差额称为货物进出口顺差,2021年我国货物进出口顺差是万亿元;(3)、写出一条关于我国货物进出口总额变化趋势的信息.19. 科学规范戴口罩是阻断新冠病毒传播的有效措施之一,某口罩生产厂家接到一公司的订单,生产一段时间后,还剩280万个口罩未生产,厂家因更换设备,生产效率比更换设备前提高了40%.结果刚好提前2天完成订单任务.求该厂家更换设备前和更换设备后每天各生产多少万个口罩?20. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题: (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).21. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且.
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).21. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且. (1)、求证:;(2)、若 , , 求的长.22. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)、求证:;(2)、若 , , 求的长.22. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.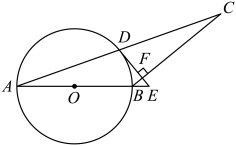 (1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.23. 如图,已知抛物线y=ax2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=-1,连接AC.
(1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.23. 如图,已知抛物线y=ax2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=-1,连接AC.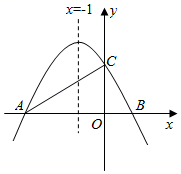 (1)、求该抛物线的表达式;(2)、若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;(3)、在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使 ,请直接写出所有符合条件的点P的坐标.24. 小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.
(1)、求该抛物线的表达式;(2)、若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;(3)、在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使 ,请直接写出所有符合条件的点P的坐标.24. 小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.如图,在中,为边上的高, , 点在边上,且 , 点是线段上任意一点,连接 , 将沿翻折得 .
 (1)、问题解决:
(1)、问题解决:如图①,当 , 将沿翻折后,使点与点重合,则;
(2)、问题探究:如图②,当 , 将沿翻折后,使 , 求的度数,并求出此时的最小值;
(3)、拓展延伸:当 , 将沿翻折后,若 , 且 , 根据题意在备用图中画出图形,并求出的值.