湖南省永州市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
1. 我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”、如:粮库把运进30吨粮食记为“”,则“”表示( )A、运出30吨粮食 B、亏损30吨粮食 C、卖掉30吨粮食 D、吃掉30吨粮食2. 企业标志反映了思想、理念等企业文化,在设计上特别注重对称美,下列企业标志图为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列多边形中,内角和等于的是( )A、
3. 下列多边形中,内角和等于的是( )A、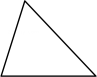 B、
B、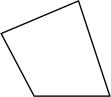 C、
C、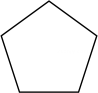 D、
D、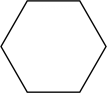 4. 关于x的一元一次方程的解为 , 则m的值为( )A、3 B、 C、7 D、5. 下列各式计算结果正确的是( )A、 B、 C、 D、6. 下列几何体中,其三视图的主视图和左视图都为三角形的是( )A、
4. 关于x的一元一次方程的解为 , 则m的值为( )A、3 B、 C、7 D、5. 下列各式计算结果正确的是( )A、 B、 C、 D、6. 下列几何体中,其三视图的主视图和左视图都为三角形的是( )A、 B、
B、 C、
C、 D、
D、 7. 某县年人均可支配收入为万元,年达到万元,若年至年间每年人均可支配收入的增长率都为 , 则下面所列方程正确的是( )A、 B、 C、 D、8. 今年2月,某班准备从《在希望的田野上》《我和我的祖国》《十送红军》三首歌曲中选择两首进行排练,参加永州市即将举办的“唱响新时代,筑梦新征程”合唱选拔赛,那么该班恰好选中前面两首歌曲的概率是( )A、 B、 C、 D、19. 已知点在反比例函数的图象上,其中a,k为常数,且﹐则点M一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )
7. 某县年人均可支配收入为万元,年达到万元,若年至年间每年人均可支配收入的增长率都为 , 则下面所列方程正确的是( )A、 B、 C、 D、8. 今年2月,某班准备从《在希望的田野上》《我和我的祖国》《十送红军》三首歌曲中选择两首进行排练,参加永州市即将举办的“唱响新时代,筑梦新征程”合唱选拔赛,那么该班恰好选中前面两首歌曲的概率是( )A、 B、 C、 D、19. 已知点在反比例函数的图象上,其中a,k为常数,且﹐则点M一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )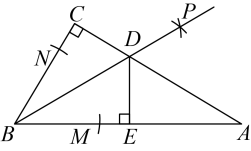 A、 B、 C、 D、一定经过的内心
A、 B、 C、 D、一定经过的内心二、填空题
-
11. , 3,三个数中最小的数为 .12. 与的公因式为 .13. 已知x为正整数,写出一个使在实数的范围内没有意义的x值是 .14. 甲、乙两队学生参加学校仪仗队选拔,两队队员的平均身高均为 , 甲队队员身高的方差为 , 乙队队员身高的方差为 , 若要求仪仗队身高比较整齐,应选择队较好.15. 如图, , 则度.
 16. 若关于x的分式方程(m为常数)有增根,则增根是 .17. 已知扇形的半径为6,面积为 , 则扇形圆心角的度数为度.18. 如图,是一个盛有水的容器的横截面,的半径为 . 水的最深处到水面的距离为 , 则水面的宽度为 .
16. 若关于x的分式方程(m为常数)有增根,则增根是 .17. 已知扇形的半径为6,面积为 , 则扇形圆心角的度数为度.18. 如图,是一个盛有水的容器的横截面,的半径为 . 水的最深处到水面的距离为 , 则水面的宽度为 .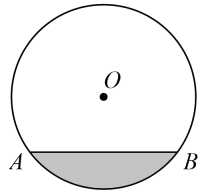
三、解答题
-
19. 解关于x的不等式组20. 先化简,再求值: , 其中.21. 如图,已知四边形是平行四边形,其对角线相交于点O, .
 (1)、是直角三角形吗?请说明理由;(2)、求证:四边形是菱形.22. 今年3月27日是第28个全国中小学生安全教育日.某市面向中小学生举行了一次关于心理健康、预防欺凌、防漏水、应急疏散等安全专题知识竞赛,共有18360名学生参加本次竞赛.为了解本次竞赛成绩情况,随机抽取了n名学生的成绩x(成绩均为整数,满分为100分)分成四个组:1组、2组、3组、4组 , 并绘制如下图所示频数分布图
(1)、是直角三角形吗?请说明理由;(2)、求证:四边形是菱形.22. 今年3月27日是第28个全国中小学生安全教育日.某市面向中小学生举行了一次关于心理健康、预防欺凌、防漏水、应急疏散等安全专题知识竞赛,共有18360名学生参加本次竞赛.为了解本次竞赛成绩情况,随机抽取了n名学生的成绩x(成绩均为整数,满分为100分)分成四个组:1组、2组、3组、4组 , 并绘制如下图所示频数分布图 (1)、;所抽取的n名学生成绩的中位数在第组;(2)、若成绩在第4组才为优秀,则所抽取的n名学生中成绩为优秀的频率为;(3)、试估计18360名参赛学生中,成绩大于或等于70分的人数.23. 永州市道县陈树湘纪念馆中陈列的陈树湘雕像高2.9米(如图1所示),寓意陈树湘为中国革命“断肠明志”牺牲时的年龄为29岁.如图2,以线段代表陈树湘雕像,一参观者在水平地面上D处为陈树湘雕拍照,相机支架高0.9米,在相机C处观测雕像顶端A的仰角为 , 然后将相机架移到处拍照,在相机M处观测雕像顶端A的仰角为 , 求D、N两点间的距离(结果精确到0.1米,参考数据:)
(1)、;所抽取的n名学生成绩的中位数在第组;(2)、若成绩在第4组才为优秀,则所抽取的n名学生中成绩为优秀的频率为;(3)、试估计18360名参赛学生中,成绩大于或等于70分的人数.23. 永州市道县陈树湘纪念馆中陈列的陈树湘雕像高2.9米(如图1所示),寓意陈树湘为中国革命“断肠明志”牺牲时的年龄为29岁.如图2,以线段代表陈树湘雕像,一参观者在水平地面上D处为陈树湘雕拍照,相机支架高0.9米,在相机C处观测雕像顶端A的仰角为 , 然后将相机架移到处拍照,在相机M处观测雕像顶端A的仰角为 , 求D、N两点间的距离(结果精确到0.1米,参考数据:) 24. 小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表的一组数据:
24. 小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表的一组数据:时间t(单位:分钟)
1
2
3
4
5
…
总水量y(单位:毫升)
7
12
17
22
27
…
(1)、探究:根据上表中的数据,请判断和(k,b为常数)哪一个能正确反映总水量y与时间t的函数关系?并求出y关于t的表达式;(2)、应用:①请你估算小明在第20分钟测量时量筒的总水量是多少毫升?
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.

