湖南省怀化市2023年中考数学试卷

试卷更新日期：2023-06-25 类型：中考真卷

进入出卷网下载

一、单选题

1. 下列四个实数中，最小的数是（）

A、 $- 5$ B、0 C、 $\frac{1}{2}$ D、 $\sqrt{2}$

查看试题解析
2. 2023年4月12日21时，正在运行的中国大科学装置“人造太阳”——世界首个全超导托卡马克东方超环（EAST）装置取得重大成果，在第122254次实验中成功实现了403秒稳态长脉冲高约束模式等离子体运行，创造了托卡马克装置高约束模式运行新的世界纪录．数据122254用科学记数法表示为（）

A、 $12.2254 \times 1 0^{4}$ B、 $1.22254 \times 1 0^{4}$ C、 $1.22254 \times 1 0^{5}$ D、 $0.122254 \times 1 0^{6}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(a b^{3})}^{2} = a^{2} b^{9}$ D、 $5 a - 2 a = 3$

查看试题解析
4. 剪纸又称刻纸，是中国最古老的民间艺术之一，它是以纸为加工对象，以剪刀（或刻刀）为工具进行创作的艺术．民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态，构成美丽的图案．下列剪纸中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 在平面直角坐标系中，点 $P (2 ， - 3)$ 关于x轴对称的点 $P^{'}$ 的坐标是（）

A、 $(- 2 ， - 3)$ B、 $(- 2 ， 3)$ C、 $(2 ， - 3)$ D、 $(2 ， 3)$

查看试题解析
6. 如图，平移直线 $A B$ 至 $C D$ ，直线 $A B$ ， $C D$ 被直线 $E F$ 所截， $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数为（）

A、 $30 °$ B、 $60 °$ C、 $100 °$ D、 $120 °$

查看试题解析
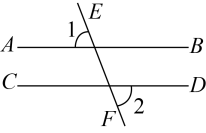7. 某县“三独”比赛独唱项目中，5名同学的得分分别是： $9.6$ ， $9.2$ ， 9.6， $9.7$ ， $9.4$ .关于这组数据，下列说法正确的是（）

A、众数是 $9.6$ B、中位数是 $9.5$ C、平均数是 $9.4$ D、方差是 $0.3$

查看试题解析
8. 下列说法错误的是（）

A、成语“水中捞月”表示的事件是不可能事件 B、一元二次方程 $x^{2} + x + 3 = 0$ 有两个相等的实数根 C、任意多边形的外角和等于 $360 °$ D、三角形三条中线的交点叫作三角形的重心

查看试题解析
9. 已知压力 $F (N)$ 、压强 $p (P a)$ 与受力面积 $S (m^{2})$ 之间有如下关系式： $F = p S$ ．当F为定值时，下图中大致表示压强p与受力面积S之间函数关系的是（）

A、 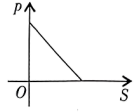B、 C、 D、

查看试题解析
10. 如图，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象与过点 $(- 1 ， 0)$ 的直线 $A B$ 相交于 $A$ 、 $B$ 两点．已知点 $A$ 的坐标为 $(1 ， 3)$ ，点 $C$ 为 $x$ 轴上任意一点．如果 $S_{△ A B C} = 9$ ，那么点 $C$ 的坐标为（）

A、 $(- 3 ， 0)$ B、 $(5 ， 0)$ C、 $(- 3 ， 0)$ 或 $(5 ， 0)$ D、 $(3 ， 0)$ 或 $(- 5 ， 0)$

查看试题解析

二、填空题

11. 要使代数式 $\sqrt{x - 9}$ 有意义，则x的取值范围是．

查看试题解析
12. 分解因式： ${2a}^{2} - 4a + 2 =$ ．

查看试题解析
13. 已知关于x的一元二次方程 $x^{2} + m x - 2 = 0$ 的一个根为 $- 1$ ，则m的值为，另一个根为．

查看试题解析
14. 定义新运算： $(a ， b) \cdot (c ， d) = a c + b d$ ，其中 $a$ ， $b$ ， $c$ ， $d$ 为实数．例如： $(1 ， 2) \cdot (3 ， 4) = 1 \times 3 + 2 \times 4 = 11$ ．如果 $(2 x ， 3) \cdot (3 ， - 1) = 3$ ，那么 $x =$ ．

查看试题解析
15. 如图，点 $P$ 是正方形 $A B C D$ 的对角线 $A C$ 上的一点， $P E ⊥ A D$ 于点 $E$ ， $P E = 3$ ．则点 $P$ 到直线 $A B$ 的距离为．

查看试题解析
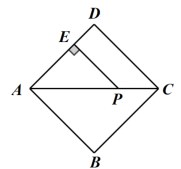16. 在平面直角坐标系中， $△ A O B$ 为等边三角形，点A的坐标为 $(1 ， 0)$ ．把 $△ A O B$ 按如图所示的方式放置，并将 $△ A O B$ 进行变换：第一次变换将 $△ A O B$ 绕着原点O顺时针旋转 $60 °$ ，同时边长扩大为 $△ A O B$ 边长的2倍，得到 $△ A_{1} O B_{1}$ ；第二次旋转将 $△ A_{1} O B_{1}$ 绕着原点O顺时针旋转 $60 °$ ，同时边长扩大为 $△ A_{1} O B_{1}$ ，边长的2倍，得到 $△ A_{2} O B_{2}$ ， …．依次类推，得到 $△ A_{2033} O B_{2033}$ ，则 $△ A_{2023} O B_{2033}$ 的边长为，点 $A_{2023}$ 的坐标为．

查看试题解析

三、解答题

17. 计算： $1 - 21 + {(\frac{1}{3})}^{- 1} - \sqrt{9} + {(s i n 45 ° - 1)}^{0} - (- 1)$

查看试题解析
18. 先化简 $(1 + \frac{3}{a - 1}) \div \frac{a^{2} - 4}{a - 1}$ ，再从 $- 1$ ， 0，1，2中选择一个适当的数作为a的值代入求值．

查看试题解析
19. 如图，矩形 $A B C D$ 中，过对角线 $B D$ 的中点 $O$ 作 $B D$ 的垂线 $E F$ ，分别交 $A D$ ， $B C$ 于点 $E$ ， $F$ ．

(1)、证明： $△ B O F ≌ △ D O E$ ；

(2)、连接 $B E$ 、 $D F$ ，证明：四边形 $E B F D$ 是菱形．

查看试题解析
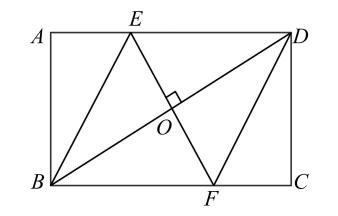20. 为弘扬革命传统精神，清明期间，某校组织学生前往怀化市烈士陵园缅怀革命先烈．大家被革命烈士纪念碑的雄伟壮观震撼，想知道纪念碑的通高 $C D$ （碑顶到水平地面的距离），于是师生组成综合实践小组进行测量．他们在地面的 $A$ 点用测角仪测得碑顶 $D$ 的仰角为 $30 °$ ，在 $B$ 点处测得碑顶 $D$ 的仰角为 $60 °$ ，已知 $A B = 35 m$ ，测角仪的高度是 $1.5 m$ （ $A$ 、 $B$ 、 $C$ 在同一直线上），根据以上数据求烈士纪念碑的通高 $C D$ ．（ $\sqrt{3} \approx 1.732$ ，结果保留一位小数）

查看试题解析
21. 近年，“青少年视力健康”受到社会的广泛关注．某校综合实践小组为了解该校学生的视力健康状况，从全校学生中随机抽取部分学生进行视力调查．根据调查结果和视力有关标准，绘制了两幅不完整的统计图．请根据图中信息解答下列问题：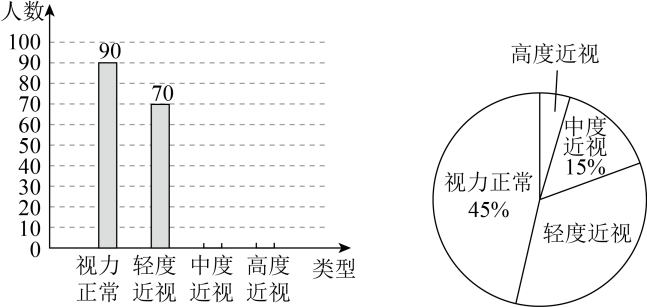

(1)、所抽取的学生人数为；

(2)、补全条形统计图，并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数；

(3)、该校共有学生 $3000$ 人，请估计该校学生中近视程度为“轻度近视”的人数．

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径，点 $P$ 是 $⊙ O$ 外一点， $P A$ 与 $⊙ O$ 相切于点 $A$ ，点 $C$ 为 $⊙ O$ 上的一点．连接 $P C$ 、 $A C$ 、 $O C$ ，且 $P C = P A$ ．

(1)、求证： $P C$ 为 $⊙ O$ 的切线；

(2)、延长 $P C$ 与 $A B$ 的延长线交于点D，求证： $P D \cdot O C = P A \cdot O D$ ；

(3)、若 $∠ C A B = 30 ° ， O D = 8$ ，求阴影部分的面积．

查看试题解析
23. 某中学组织学生研学，原计划租用可坐乘客 $45$ 人的 $A$ 种客车若干辆，则有 $30$ 人没有座位；若租用可坐乘客 $60$ 人的 $B$ 种客车，则可少租 $6$ 辆，且恰好坐满．

(1)、求原计划租用 $A$ 种客车多少辆？这次研学去了多少人？

(2)、若该校计划租用 $A$ 、 $B$ 两种客车共 $25$ 辆，要求 $B$ 种客车不超过 $7$ 辆，且每人都有座位，则有哪几种租车方案？

(3)、在（2）的条件下，若 $A$ 种客车租金为每辆 $220$ 元， $B$ 种客车租金每辆 $300$ 元，应该怎样租车才最合算？

查看试题解析
24. 如图一所示，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 8$ 与 $x$ 轴交于 $A (- 4 ， 0) 、 B (2 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的函数表达式及顶点坐标；

(2)、点 $P$ 为第三象限内抛物线上一点，作直线 $A C$ ，连接 $P A$ 、 $P C$ ，求 $△ P A C$ 面积的最大值及此时点 $P$ 的坐标；

(3)、设直线 $l_{1} ： y = k x + k - \frac{35}{4}$ 交抛物线于点 $M$ 、 $N$ ，求证：无论 $k$ 为何值，平行于 $x$ 轴的直线 $l_{2} ： y = - \frac{37}{4}$ 上总存在一点 $E$ ，使得 $∠ M E N$ 为直角．

查看试题解析