甘肃省武威、平凉、天水、白银、定西、张掖、陇南、金昌、酒泉、庆阳2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
1. 9的算术平方根是( )A、 B、 C、3 D、2. 若 , 则( )A、6 B、 C、1 D、3. 计算:( )A、2 B、 C、 D、4. 若直线(是常数,)经过第一、第三象限,则的值可为( )A、 B、 C、 D、25. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( )
 A、 B、 C、 D、6. 方程的解为( )A、 B、 C、 D、7. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( )
A、 B、 C、 D、6. 方程的解为( )A、 B、 C、 D、7. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( ) A、2 B、4 C、5 D、68. 据统计,数学家群体是一个长寿群体,某研究小组随机抽取了收录约位数学家的《数学家传略辞典》中部分岁及以上的长寿数学家的年龄为样本,对数据进行整理与分析,统计图表(部分数据)如下,下列结论错误的是( )
A、2 B、4 C、5 D、68. 据统计,数学家群体是一个长寿群体,某研究小组随机抽取了收录约位数学家的《数学家传略辞典》中部分岁及以上的长寿数学家的年龄为样本,对数据进行整理与分析,统计图表(部分数据)如下,下列结论错误的是( )年龄范围(岁)
人数(人)
25


11
10
 A、该小组共统计了100名数学家的年龄 B、统计表中的值为5 C、长寿数学家年龄在岁的人数最多 D、《数学家传略辞典》中收录的数学家年龄在岁的人数估计有110人9. 如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( )
A、该小组共统计了100名数学家的年龄 B、统计表中的值为5 C、长寿数学家年龄在岁的人数最多 D、《数学家传略辞典》中收录的数学家年龄在岁的人数估计有110人9. 如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线与地面所成夹角时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜与地面的夹角( ) A、 B、 C、 D、10. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )
A、 B、 C、 D、10. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )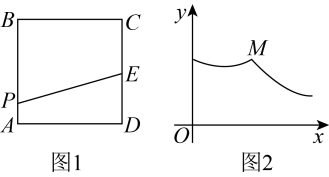 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
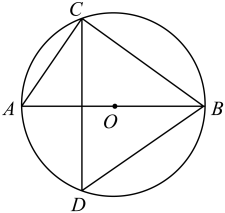
11. 因式分解: .12. 关于的一元二次方程有两个不相等的实数根,则(写出一个满足条件的值).13. 近年来,我国科技工作者践行“科技强国”使命,不断取得世界级的科技成果,如由我国研制的中国首台作业型全海深自主遥控潜水器“海斗一号”,最大下潜深度10907米,填补了中国水下万米作业型无人潜水器的空白;由我国自主研发的极目一号Ⅲ型浮空艇“大白鲸”,升空高度至海拔9050米,创造了浮空艇原位大气科学观测海拔最高的世界记录.如果把海平面以上9050米记作“米”,那么海平面以下10907米记作“米”.14. 如图,内接于 , 是的直径,点是上一点, , 则 .
 15. 如图,菱形中, , , , 垂足分别为 , , 若 , 则 .
15. 如图,菱形中, , , , 垂足分别为 , , 若 , 则 .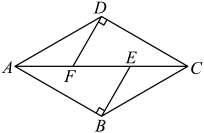 16. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留)
16. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留)
三、解答题
-
17. 计算: .18. 解不等式组:19. 化简: .20. 1672年,丹麦数学家莫尔在他的著作《欧几里得作图》中指出:只用圆规可以完成一切尺规作图.1797年,意大利数学家马斯凯罗尼又独立发现此结论,并写在他的著作《圆规的几何学》中.请你利用数学家们发现的结论,完成下面的作图题:
如图,已知 , 是上一点,只用圆规将的圆周四等分.(按如下步骤完成,保留作图痕迹)

①以点为圆心,长为半径,自点起,在上逆时针方向顺次截取;
②分别以点 , 点为圆心,长为半径作弧,两弧交于上方点;
③以点为圆心,长为半径作弧交于 , 两点.即点 , , , 将的圆周四等分.
21. 为传承红色文化,激发革命精神,增强爱国主义情感,某校组织七年级学生开展“讲好红色故事,传承红色基因”为主题的研学之旅,策划了三条红色线路让学生选择:A.南梁精神红色记忆之旅(华池县);B.长征会师胜利之旅(会宁县);C.西路军红色征程之旅(高台县),且每人只能选择一条线路.小亮和小刚两人用抽卡片的方式确定一条自己要去的线路.他们准备了3张不透明的卡片,正面分别写上字母 , , , 卡片除正面字母不同外其余均相同,将3张卡片正面向下洗匀,小亮先从中随机抽取一张卡片,记下字母后正面向下放回,洗匀后小刚再从中随机抽取一张卡片.
(1)、求小亮从中随机抽到卡片的概率;(2)、请用画树状图或列表的方法,求两人都抽到卡片的概率.22. 如图1,某人的一器官后面处长了一个新生物,现需检测到皮肤的距离(图1).为避免伤害器官,可利用一种新型检测技术,检测射线可避开器官从侧面测量.某医疗小组制定方案,通过医疗仪器的测量获得相关数据,并利用数据计算出新生物到皮肤的距离.方案如下:课题
检测新生物到皮肤的距离
工具
医疗仪器等
示意图
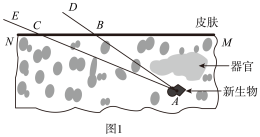

说明
如图2,新生物在处,先在皮肤上选择最大限度地避开器官的处照射新生物,检测射线与皮肤的夹角为;再在皮肤上选择距离处的处照射新生物,检测射线与皮肤的夹角为 .
测量数据
, ,
请你根据上表中的测量数据,计算新生物处到皮肤的距离.(结果精确到)(参考数据: , , , , , )
23. 某校八年级共有200名学生,为了解八年级学生地理学科的学习情况,从中随机抽取40名学生的八年级上、下两个学期期末地理成绩进行整理和分析(两次测试试卷满分均为35分,难度系数相同;成绩用表示,分成6个等级: . ; . ; . ; . ; . ; . ).下面给出了部分信息:a.八年级学生上、下两个学期期末地理成绩的统计图如下:

b.八年级学生上学期期末地理成绩在 . 这一组的成绩是:
15,15,15,15,15,16,16,16,18,18
c.八年级学生上、下两个学期期末地理成绩的平均数、众数、中位数如下:
学期
平均数
众数
中位数
八年级上学期
15
八年级下学期
19
根据以上信息,回答下列问题:
(1)、填空:;(2)、若为优秀,则这200名学生八年级下学期期末地理成绩达到优秀的约有人;(3)、你认为该校八年级学生的期末地理成绩下学期比上学期有没有提高?请说明理由.24. 如图,一次函数的图象与轴交于点 , 与反比例函数的图象交于点 . (1)、求点的坐标;(2)、用的代数式表示;(3)、当的面积为9时,求一次函数的表达式.25. 如图,内接于 , 是的直径,是上的一点,平分 , , 垂足为 , 与相交于点 .
(1)、求点的坐标;(2)、用的代数式表示;(3)、当的面积为9时,求一次函数的表达式.25. 如图,内接于 , 是的直径,是上的一点,平分 , , 垂足为 , 与相交于点 . (1)、求证:是的切线;(2)、当的半径为 , 时,求的长.26.
(1)、求证:是的切线;(2)、当的半径为 , 时,求的长.26.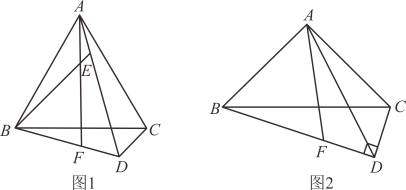 (1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.
(1)、【模型建立】如图1,和都是等边三角形,点关于的对称点在边上.①求证:;
②用等式写出线段 , , 的数量关系,并说明理由.
(2)、【模型应用】如图2,是直角三角形, , , 垂足为 , 点关于的对称点在边上.用等式写出线段 , , 的数量关系,并说明理由.
(3)、【模型迁移】在(2)的条件下,若 , , 求的值.
27. 如图1,抛物线与轴交于点 , 与直线交于点 , 点在轴上.点从点出发,沿线段方向匀速运动,运动到点时停止. (1)、求抛物线的表达式;(2)、当时,请在图1中过点作交抛物线于点 , 连接 , , 判断四边形的形状,并说明理由.(3)、如图2,点从点开始运动时,点从点同时出发,以与点相同的速度沿轴正方向匀速运动,点停止运动时点也停止运动.连接 , , 求的最小值.
(1)、求抛物线的表达式;(2)、当时,请在图1中过点作交抛物线于点 , 连接 , , 判断四边形的形状,并说明理由.(3)、如图2,点从点开始运动时,点从点同时出发,以与点相同的速度沿轴正方向匀速运动,点停止运动时点也停止运动.连接 , , 求的最小值.