上海市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 在分式方程中,设 , 可得到关于y的整式方程为( )A、 B、 C、 D、3. 下列函数中,函数值y随x的增大而减小的是( )A、 B、 C、 D、4. 如图所示,为了调查不同时间段的车流量,某学校的兴趣小组统计了不同时间段的车流量,下图是各时间段的小车与公车的车流量,则下列说法正确的是( )
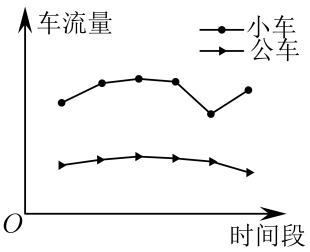 A、小车的车流量与公车的车流量稳定; B、小车的车流量的平均数较大; C、小车与公车车流量在同一时间段达到最小值; D、小车与公车车流量的变化趋势相同.5. 在四边形中, . 下列说法能使四边形为矩形的是( )A、 B、 C、 D、6. 已知在梯形中,连接 , 且 , 设 . 下列两个说法:
A、小车的车流量与公车的车流量稳定; B、小车的车流量的平均数较大; C、小车与公车车流量在同一时间段达到最小值; D、小车与公车车流量的变化趋势相同.5. 在四边形中, . 下列说法能使四边形为矩形的是( )A、 B、 C、 D、6. 已知在梯形中,连接 , 且 , 设 . 下列两个说法:①;②
则下列说法正确的是( )
A、①正确②错误 B、①错误②正确 C、①②均正确 D、①②均错误二、填空题
-
7. 分解因式: .8. 化简:的结果为 .9. 已知关于的方程 , 则10. 函数的定义域为 .11. 已知关于x的一元二次方程没有实数根,那么a的取值范围是 .12. 在不透明的盒子中装有一个黑球,两个白球,三个红球,四个绿球,这十个球除颜色外完全相同.那么从中随机摸出一个球是绿球的概率为 .13. 如果一个正多边形的中心角是 , 那么这个正多边形的边数为 .14. 一个二次函数的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是 .15. 如图,在中,点D,E在边 , 上, , 连结 , 设向量 , , 那么用 , 表示 .
 16. 垃圾分类(Refuse sorting),是指按照垃圾的不同成分、属性、利用价值以及对环境的影响,并根据不同处置方式的要求,分成属性不同的若干种类.某市试点区域的垃圾收集情况如扇形统计图所示,已知可回收垃圾共收集60 吨,且全市人口约为试点区域人口的10倍,那么估计全市可收集的干垃圾总量为 .
16. 垃圾分类(Refuse sorting),是指按照垃圾的不同成分、属性、利用价值以及对环境的影响,并根据不同处置方式的要求,分成属性不同的若干种类.某市试点区域的垃圾收集情况如扇形统计图所示,已知可回收垃圾共收集60 吨,且全市人口约为试点区域人口的10倍,那么估计全市可收集的干垃圾总量为 .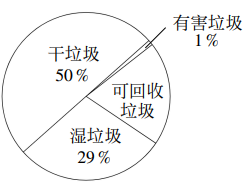 17. 如图,在中, , 将绕着点A旋转 , 旋转后的点B落在上,点B的对应点为D,连接是的角平分线,则 .
17. 如图,在中, , 将绕着点A旋转 , 旋转后的点B落在上,点B的对应点为D,连接是的角平分线,则 . 18. 在中 , 点D在边上,点E在延长线上,且 , 如果过点A,过点D,若与有公共点,那么半径r的取值范围是 .
18. 在中 , 点D在边上,点E在延长线上,且 , 如果过点A,过点D,若与有公共点,那么半径r的取值范围是 .三、解答题
-
19. 计算:20. 解不等式组21. 如图,在中,弦的长为8,点C在延长线上,且 .
 (1)、求的半径;(2)、求的正切值.22. “中国石化”推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.(1)、他实际花了多少钱购买会员卡?(2)、减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数解析式(不用写出定义域)(3)、油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元?23. 如图,在梯形中 , 点F,E分别在线段 , 上,且 ,
(1)、求的半径;(2)、求的正切值.22. “中国石化”推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.(1)、他实际花了多少钱购买会员卡?(2)、减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数解析式(不用写出定义域)(3)、油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元?23. 如图,在梯形中 , 点F,E分别在线段 , 上,且 , (1)、求证:(2)、若 , 求证:24. 在平面直角坐标系中,已知直线与x轴交于点A,y轴交于点B,点C在线段上,以点C为顶点的抛物线M:经过点B.
(1)、求证:(2)、若 , 求证:24. 在平面直角坐标系中,已知直线与x轴交于点A,y轴交于点B,点C在线段上,以点C为顶点的抛物线M:经过点B. (1)、求点A,B的坐标;(2)、求b,c的值;(3)、平移抛物线M至N,点C,B分别平移至点P,D,联结 , 且轴,如果点P在x轴上,且新抛物线过点B,求抛物线N的函数解析式.25. 如图(1)所示,已知在中, , 在边上,点边中点,为以为圆心,为半径的圆分别交 , 于点 , , 联结交于点 .
(1)、求点A,B的坐标;(2)、求b,c的值;(3)、平移抛物线M至N,点C,B分别平移至点P,D,联结 , 且轴,如果点P在x轴上,且新抛物线过点B,求抛物线N的函数解析式.25. 如图(1)所示,已知在中, , 在边上,点边中点,为以为圆心,为半径的圆分别交 , 于点 , , 联结交于点 . (1)、如果 , 求证:四边形为平行四边形;(2)、如图(2)所示,联结 , 如果 , 求边的长;(3)、联结 , 如果是以为腰的等腰三角形,且 , 求的值.
(1)、如果 , 求证:四边形为平行四边形;(2)、如图(2)所示,联结 , 如果 , 求边的长;(3)、联结 , 如果是以为腰的等腰三角形,且 , 求的值.