天津市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
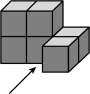
1. 计算的结果等于( )A、 B、 C、 D、12. 估计 的值应在 ( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间3. 如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、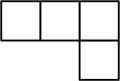 C、
C、 D、
D、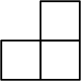 4. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、全 B、面 C、发 D、展5. 据年月日《天津日报》报道,在天津举办的第七届世界智能大会通过“百网同播、万人同屏、亿人同观”,全球网友得以共享高端思想盛宴,总浏览量达到人次,将数据用科学记数法表示应为( )A、 B、 C、 D、6. 的值等于( )A、1 B、 C、 D、27. 计算的结果等于( )A、 B、 C、 D、8. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、9. 若是方程的两个根,则( )A、 B、 C、 D、10. 如图,在中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线分别与边相交于点D,E,连接 . 若 , 则的长为( )
4. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、全 B、面 C、发 D、展5. 据年月日《天津日报》报道,在天津举办的第七届世界智能大会通过“百网同播、万人同屏、亿人同观”,全球网友得以共享高端思想盛宴,总浏览量达到人次,将数据用科学记数法表示应为( )A、 B、 C、 D、6. 的值等于( )A、1 B、 C、 D、27. 计算的结果等于( )A、 B、 C、 D、8. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、9. 若是方程的两个根,则( )A、 B、 C、 D、10. 如图,在中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线分别与边相交于点D,E,连接 . 若 , 则的长为( ) A、9 B、8 C、7 D、611. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )
A、9 B、8 C、7 D、611. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )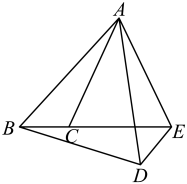 A、 B、 C、 D、12. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:
A、 B、 C、 D、12. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为 .
其中,正确结论的个数是( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 不透明袋子中装有10个球,其中有7个绿球、3个红球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是绿球的概率为 .14. 计算的结果为 .15. 计算的结果为 .16. 若直线向上平移3个单位长度后经过点 , 则的值为 .17. 如图,在边长为3的正方形的外侧,作等腰三角形 , .
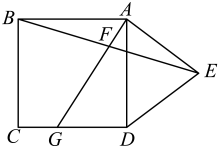 (1)、的面积为;(2)、若F为的中点,连接并延长,与相交于点G,则的长为 .
(1)、的面积为;(2)、若F为的中点,连接并延长,与相交于点G,则的长为 .三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
 (1)、线段的长为;(2)、若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .19. 解不等式组
(1)、线段的长为;(2)、若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .19. 解不等式组请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: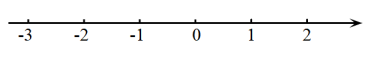 (4)、原不等式组的解集为 .20. 为培养青少年的劳动意识,某校开展了剪纸、编织、烘焙等丰富多彩的活动,该校为了解参加活动的学生的年龄情况,随机调查了名参加活动的学生的年龄(单位:岁).根据统计的结果,绘制出如下的统计图①和图②.
(4)、原不等式组的解集为 .20. 为培养青少年的劳动意识,某校开展了剪纸、编织、烘焙等丰富多彩的活动,该校为了解参加活动的学生的年龄情况,随机调查了名参加活动的学生的年龄(单位:岁).根据统计的结果,绘制出如下的统计图①和图②.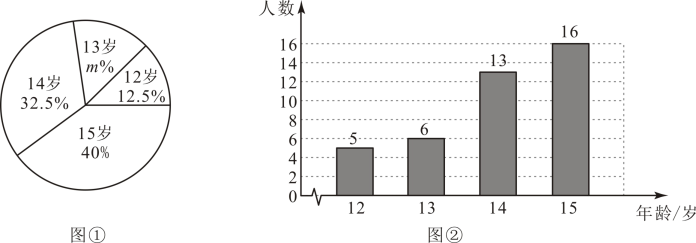
请根据相关信息,解答下列问题:
(1)、填空:a的值为 , 图①中的值为;(2)、求统计的这组学生年龄数据的平均数、众数和中位数.21. 在中,半径垂直于弦 , 垂足为D, , E为弦所对的优弧上一点.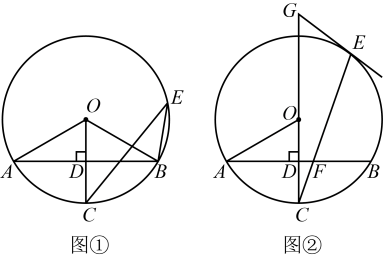 (1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.22. 综合与实践活动中,要利用测角仪测量塔的高度.
(1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.22. 综合与实践活动中,要利用测角仪测量塔的高度.如图,塔前有一座高为的观景台,已知 , 点E,C,A在同一条水平直线上.
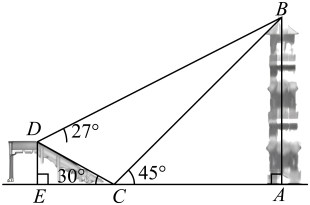
某学习小组在观景台C处测得塔顶部B的仰角为 , 在观景台D处测得塔顶部B的仰角为 .
(1)、求的长;(2)、设塔的高度为h(单位:m).①用含有h的式子表示线段的长(结果保留根号);
②求塔的高度(取0.5,取1.7,结果取整数).
23. 已知学生宿舍、文具店、体育场依次在同一条直线上,文具店离宿舍 , 体育场离宿舍 , 张强从宿舍出发,先用了匀速跑步去体育场,在体育场锻炼了 , 之后匀速步行了到文具店买笔,在文具店停留后,用了匀速散步返回宿舍.下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.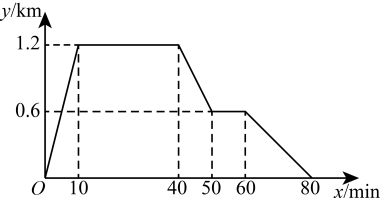
请根据相关信息,回答下列问题:
(1)、①填表:张强离开宿舍的时间/
1
10
20
60
张强离宿舍的距离/
1.2
②填空:张强从体育场到文具店的速度为;
③当时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)、当张强离开体育场时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为 , 那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)24. 在平面直角坐标系中,O为原点,菱形的顶点 , 矩形的顶点 .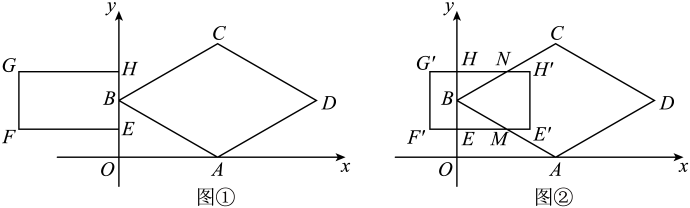 (1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.
(1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.①如图②,当边与相交于点M、边与相交于点N,且矩形与菱形重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当时,求S的取值范围(直接写出结果即可).
25. 已知抛物线 , 为常数,的顶点为 , 与轴相交于 , 两点点在点的左侧 , 与轴相交于点 , 抛物线上的点的横坐标为 , 且 , 过点作 , 垂足为 .(1)、若 .①求点和点的坐标;
②当时,求点的坐标;
(2)、若点的坐标为 , 且 , 当时,求点的坐标.