湖南省岳阳市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列运算结果正确的是( )A、 B、 C、 D、3. 下列几何体的主视图是圆的是( )A、
 B、
B、 C、
C、 D、
D、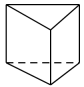 4. 已知 , 点在直线上,点在直线上,于点 , 则的度数是( )
4. 已知 , 点在直线上,点在直线上,于点 , 则的度数是( )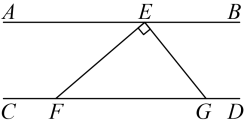 A、 B、 C、 D、5. 在5月份跳绳训练中,妍妍同学一周成绩记录如下:(单位:次/分钟),这组数据的众数和中位数分别是( )A、 B、 C、 D、6. 下列命题是真命题的是( )A、同位角相等 B、菱形的四条边相等 C、正五边形是中心对称图形 D、单项式的次数是47. 我国古代数学名著《九章算术》中有这样一道题:“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何?”结合右图,其大意是:今有圆形材质,直径为25寸,要做成方形板材,使其厚度达到7寸.则的长是( )
A、 B、 C、 D、5. 在5月份跳绳训练中,妍妍同学一周成绩记录如下:(单位:次/分钟),这组数据的众数和中位数分别是( )A、 B、 C、 D、6. 下列命题是真命题的是( )A、同位角相等 B、菱形的四条边相等 C、正五边形是中心对称图形 D、单项式的次数是47. 我国古代数学名著《九章算术》中有这样一道题:“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何?”结合右图,其大意是:今有圆形材质,直径为25寸,要做成方形板材,使其厚度达到7寸.则的长是( )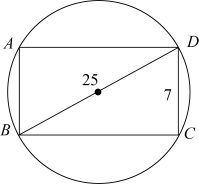 A、寸 B、25寸 C、24寸 D、7寸8. 若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.若关于的二次函数(为常数,)总有两个不同的倍值点,则的取值范围是( )A、 B、 C、 D、
A、寸 B、25寸 C、24寸 D、7寸8. 若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.若关于的二次函数(为常数,)总有两个不同的倍值点,则的取值范围是( )A、 B、 C、 D、二、填空题
-
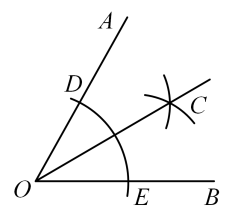
9. 函数y= 中,自变量x的取值范围是 .10. 近年来,岳阳扛牢“守护好一江碧水”责任,水在变清,岸在变绿,洞庭湖真正成为鸟类的天堂.2022年冬季,洞庭湖区越冬水鸟数量达万只,数据用科学记数法表示为 .11. 有两个女生小合唱队,各由6名队员组成,甲队与乙队的平均身高均为 , 甲队身高方差 , 乙队身高方差 , 两队身高比较整齐的是队.(填“甲”或“乙”)12. 如图,①在上分别截取线段 , 使;②分别以为圆心,以大于的长为半径画弧,在内两弧交于点;③作射线 . 若 , 则 .
 13. 观察下列式子:
13. 观察下列式子:;;;;;…
依此规律,则第(为正整数)个等式是 .
14. 已知关于的一元二次方程有两个不相等的实数根,且 , 则实数 .15. 2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在处用仪器测得赛场一宣传气球顶部处的仰角为 , 仪器与气球的水平距离为20米,且距地面高度为1.5米,则气球顶部离地面的高度是米(结果精确到0.1米,). 16. 如图,在中,为直径,为弦,点为的中点,以点为切点的切线与的延长线交于点 .
16. 如图,在中,为直径,为弦,点为的中点,以点为切点的切线与的延长线交于点 .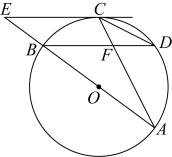 (1)、若 , 则的长是(结果保留);(2)、若 , 则 .
(1)、若 , 则的长是(结果保留);(2)、若 , 则 .三、解答题
-
17. 计算: .18. 解不等式组:19. 如图,反比例函数(为常数,)与正比例函数(为常数,)的图象交于两点.
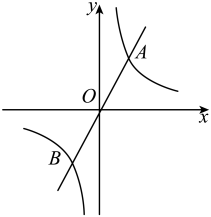 (1)、求反比例函数和正比例函数的表达式;(2)、若y轴上有一点的面积为4,求点的坐标.20. 为落实中共中央办公厅、国务院办公厅印发的《关于实施中华优秀传统文化传承发展工程意见》,深入开展“我们的节日”主题活动,某校七年级在端午节来临之际,成立了四个社团:A包粽子,B腌咸蛋,C酿甜酒,D摘艾叶.每人只参加一个社团的情况下,随机调查了部分学生,根据调查结果绘制了两幅不完整的统计图:
(1)、求反比例函数和正比例函数的表达式;(2)、若y轴上有一点的面积为4,求点的坐标.20. 为落实中共中央办公厅、国务院办公厅印发的《关于实施中华优秀传统文化传承发展工程意见》,深入开展“我们的节日”主题活动,某校七年级在端午节来临之际,成立了四个社团:A包粽子,B腌咸蛋,C酿甜酒,D摘艾叶.每人只参加一个社团的情况下,随机调查了部分学生,根据调查结果绘制了两幅不完整的统计图: (1)、本次共调查了名学生;(2)、请补全条形统计图;(3)、学校计划从四个社团中任选两个社团进行成果展示,请用列表或画树状图的方法,求同时选中A和C两个社团的概率.21. 如图,点在的边上, , 请从以下三个选项中①;②;③ , 选择一个合适的选项作为已知条件,使为矩形.
(1)、本次共调查了名学生;(2)、请补全条形统计图;(3)、学校计划从四个社团中任选两个社团进行成果展示,请用列表或画树状图的方法,求同时选中A和C两个社团的概率.21. 如图,点在的边上, , 请从以下三个选项中①;②;③ , 选择一个合适的选项作为已知条件,使为矩形.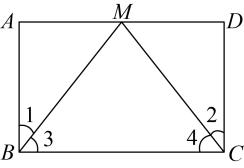 (1)、你添加的条件是(填序号);(2)、添加条件后,请证明为矩形.22. 水碧万物生,岳阳龙虾好.小龙虾产业已经成为岳阳乡村振兴的“闪亮名片”.已知翠翠家去年龙虾的总产量是 , 今年龙虾的总产量是 , 且去年与今年的养殖面积相同,平均亩产量去年比今年少 , 求今年龙虾的平均亩产量.23. 如图1,在中, , 点分别为边的中点,连接 .
(1)、你添加的条件是(填序号);(2)、添加条件后,请证明为矩形.22. 水碧万物生,岳阳龙虾好.小龙虾产业已经成为岳阳乡村振兴的“闪亮名片”.已知翠翠家去年龙虾的总产量是 , 今年龙虾的总产量是 , 且去年与今年的养殖面积相同,平均亩产量去年比今年少 , 求今年龙虾的平均亩产量.23. 如图1,在中, , 点分别为边的中点,连接 . (1)、初步尝试:与的数量关系是 , 与的位置关系是 .(2)、特例研讨:如图2,若 , 先将绕点顺时针旋转(为锐角),得到 , 当点在同一直线上时,与相交于点 , 连接 .
(1)、初步尝试:与的数量关系是 , 与的位置关系是 .(2)、特例研讨:如图2,若 , 先将绕点顺时针旋转(为锐角),得到 , 当点在同一直线上时,与相交于点 , 连接 .①求的度数;
②求的长.
(3)、深入探究:若 , 将绕点顺时针旋转 , 得到 , 连接 , . 当旋转角满足 , 点在同一直线上时,利用所提供的备用图探究与的数量关系,并说明理由.24. 已知抛物线与轴交于两点,交轴于点 . (1)、请求出抛物线的表达式.(2)、如图1,在轴上有一点 , 点在抛物线上,点为坐标平面内一点,是否存在点使得四边形为正方形?若存在,请求出点的坐标;若不存在,请说明理由.(3)、如图2,将抛物线向右平移2个单位,得到抛物线 , 抛物线的顶点为 , 与轴正半轴交于点 , 抛物线上是否存在点 , 使得?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、请求出抛物线的表达式.(2)、如图1,在轴上有一点 , 点在抛物线上,点为坐标平面内一点,是否存在点使得四边形为正方形?若存在,请求出点的坐标;若不存在,请说明理由.(3)、如图2,将抛物线向右平移2个单位,得到抛物线 , 抛物线的顶点为 , 与轴正半轴交于点 , 抛物线上是否存在点 , 使得?若存在,请求出点的坐标;若不存在,请说明理由.