山东省枣庄市2023年中考数学试卷
试卷更新日期:2023-06-25 类型:中考真卷
一、单选题
-
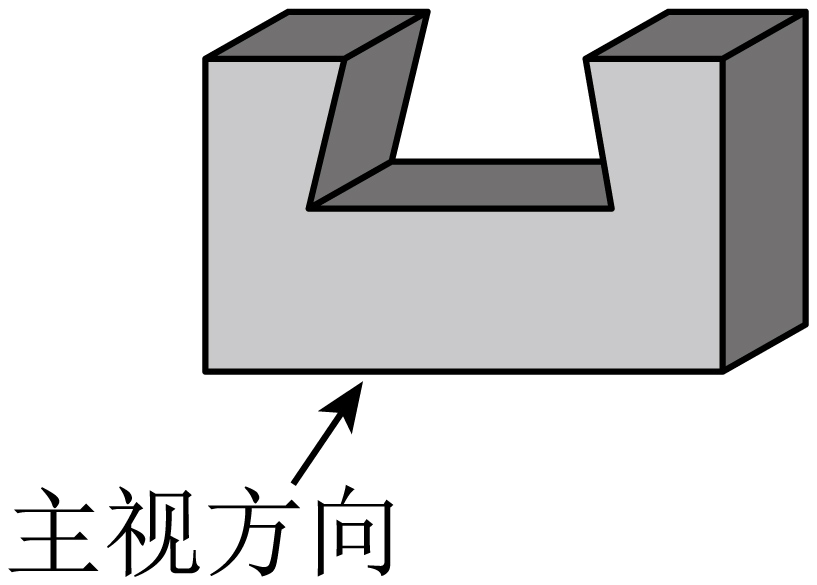
1. 下列各数中比1大的数是( )A、2 B、0 C、-1 D、-32. 榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
 A、
A、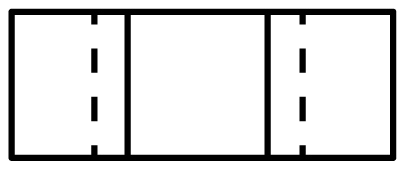 B、
B、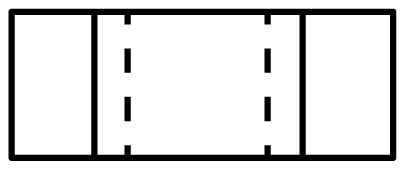 C、
C、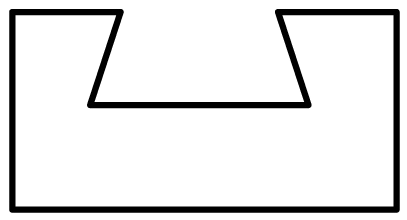 D、
D、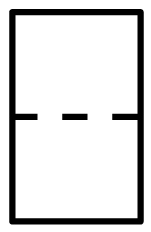 3. 随着全球新一轮科技革命和产业变革的蓬勃发展,新能源汽车已经成为全球汽车产业转型发展的主要方向,根据中国乘用车协会的统计数据,2023年第一季度,中国新能源汽车销量为159万辆,同比增长 , 其中159万用科学记数法表示为( )A、 B、 C、 D、4. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x天可以追上慢马,则下列方程正确的是( )A、 B、 C、 D、5. 下列运算结果正确的是( )A、 B、 C、 D、6. 4月23日是世界读书日,学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:
3. 随着全球新一轮科技革命和产业变革的蓬勃发展,新能源汽车已经成为全球汽车产业转型发展的主要方向,根据中国乘用车协会的统计数据,2023年第一季度,中国新能源汽车销量为159万辆,同比增长 , 其中159万用科学记数法表示为( )A、 B、 C、 D、4. 我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x天可以追上慢马,则下列方程正确的是( )A、 B、 C、 D、5. 下列运算结果正确的是( )A、 B、 C、 D、6. 4月23日是世界读书日,学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:人数
6
7
10
7
课外书数量(本)
6
7
9
12
则阅读课外书数量的中位数和众数分别是( )
A、8,9 B、10,9 C、7,12 D、9,97. 如图,在中,弦相交于点P,若 , 则的度数为( ) A、 B、 C、 D、8. 如图,一束太阳光线平行照射在放置于地面的正六边形上,若 , 则的度数为( )
A、 B、 C、 D、8. 如图,一束太阳光线平行照射在放置于地面的正六边形上,若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在中, , 以点A为圆心,以的长为半径作弧交于点D,连接 , 再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线交于点E,连接 , 则下列结论中不正确的是( )
A、 B、 C、 D、9. 如图,在中, , 以点A为圆心,以的长为半径作弧交于点D,连接 , 再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线交于点E,连接 , 则下列结论中不正确的是( ) A、 B、 C、 D、10. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( )
A、 B、 C、 D、10. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 计算 .12. 若是关x的方程的解,则的值为 .13. 银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图是一片银杏叶标本,叶片上两点B,C的坐标分别为 , 将银杏叶绕原点顺时针旋转后,叶柄上点A对应点的坐标为 .
 14. 如图所示,桔棒是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆米, , 支架米,可以绕着点O自由旋转,当点A旋转到如图所示位置时 , 此时点B到水平地面的距离为米.(结果保留根号)
14. 如图所示,桔棒是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆米, , 支架米,可以绕着点O自由旋转,当点A旋转到如图所示位置时 , 此时点B到水平地面的距离为米.(结果保留根号) 15. 如图,在正方形中,对角线与相交于点O,E为上一点, , F为的中点,若的周长为32,则的长为 .
15. 如图,在正方形中,对角线与相交于点O,E为上一点, , F为的中点,若的周长为32,则的长为 . 16. 如图,在反比例函数的图象上有等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , 则 .
16. 如图,在反比例函数的图象上有等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为 , 则 .
三、解答题
-
17. 先化简,再求值: , 其中a的值从不等式组的解集中选取一个合适的整数.18.(1)、观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征: , .
 (2)、动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
(2)、动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征. 19. 对于任意实数a,b,定义一种新运算: , 例如: , . 根据上面的材料,请完成下列问题:(1)、 , ;(2)、若 , 求x的值.20. 《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学的一门独立课程,日常生活劳动设定四个任务群:A清洁与卫生,B整理与收纳,C家用器具使用与维护,D烹饪与营养.学校为了较好地开设课程,对学生最喜欢的任务群进行了调查,并将调查结果绘制成以下两幅不完整的统计图.
19. 对于任意实数a,b,定义一种新运算: , 例如: , . 根据上面的材料,请完成下列问题:(1)、 , ;(2)、若 , 求x的值.20. 《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学的一门独立课程,日常生活劳动设定四个任务群:A清洁与卫生,B整理与收纳,C家用器具使用与维护,D烹饪与营养.学校为了较好地开设课程,对学生最喜欢的任务群进行了调查,并将调查结果绘制成以下两幅不完整的统计图.
请根据统计图解答下列问题:
(1)、本次调查中,一共调查了名学生,其中选择“C家用器具使用与维护”的女生有名,“D烹饪与营养”的男生有名.(2)、补全上面的条形统计图和扇形统计图;(3)、学校想从选择“C家用器具使用与维护”的学生中随机选取两名学生作为“家居博览会”的志愿者,请用画树状图或列表法求出所选的学生恰好是一名男生和一名女生的概率.21. 如图,一次函数的图象与反比例函数的图象交于两点. (1)、求一次函数的表达式,并在所给的平面直角坐标系中画出这个一次函数的图象;(2)、观察图象,直接写出不等式的解集;(3)、设直线与x轴交于点C,若为y轴上的一动点,连接 , 当的面积为时,求点P的坐标.22. 如图,为的直径,点C是的中点,过点C做射线的垂线,垂足为E.
(1)、求一次函数的表达式,并在所给的平面直角坐标系中画出这个一次函数的图象;(2)、观察图象,直接写出不等式的解集;(3)、设直线与x轴交于点C,若为y轴上的一动点,连接 , 当的面积为时,求点P的坐标.22. 如图,为的直径,点C是的中点,过点C做射线的垂线,垂足为E. (1)、求证:是切线;(2)、若 , 求的长;(3)、在(2)的条件下,求阴影部分的面积(用含有的式子表示).23. 如图,抛物线经过两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与轴交于点D.
(1)、求证:是切线;(2)、若 , 求的长;(3)、在(2)的条件下,求阴影部分的面积(用含有的式子表示).23. 如图,抛物线经过两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与轴交于点D. (1)、求该抛物线的表达式;(2)、若点H是x轴上一动点,分别连接MH,DH,求的最小值;(3)、若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.24. 问题情境:如图1,在中, , 是边上的中线.如图2,将的两个顶点B,C分别沿折叠后均与点D重合,折痕分别交于点E,G,F,H.
(1)、求该抛物线的表达式;(2)、若点H是x轴上一动点,分别连接MH,DH,求的最小值;(3)、若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.24. 问题情境:如图1,在中, , 是边上的中线.如图2,将的两个顶点B,C分别沿折叠后均与点D重合,折痕分别交于点E,G,F,H. (1)、 猜想证明:
(1)、 猜想证明:如图2,试判断四边形的形状,并说明理由.
(2)、 问题解决;如图3,将图2中左侧折叠的三角形展开后,重新沿折叠,使得顶点B与点H重合,折痕分别交于点M,N,的对应线段交于点K,求四边形的面积.