江西省上饶市鄱阳县2022-2023学年七年级下学期数学期中考试试卷

试卷更新日期：2023-06-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标，其中可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 已知点P的坐标为 $(3 ， - 1)$ ，则点P位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列实数 $3 π$ ， $- \frac{7}{8}$ ，0， $\sqrt{2}$ ， $- 3.15$ ， $\sqrt{9}$ ， $\frac{\sqrt{3}}{3}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，点 $E$ 在 $C D$ 延长线上，下列条件中不能判定 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 5 = ∠ B$ D、 $∠ B + ∠ B D C = 180 °$

查看试题解析
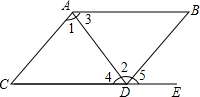5. 下列语句中真命题有（）①点到直线的垂线段叫做点到直线的距离；②内错角相等；③两点之间线段最短；④过一点有且只有一条直线与已知直线平行；⑤在同一平面内，若两条直线都与第三条直线垂直，则这两条直线互相平行．

A、5个 B、4个 C、3个 D、2个

查看试题解析
6. 如图，将边长为 $1$ 的正方形依次放在坐标系中，其中第一个正方形的两边 $O A_{1}$ ， $O A_{3}$ 分别在 $y$ 轴和 $x$ 轴上，第二个正方形的一边 $A_{3} A_{4}$ 与第一个正方形的边 $A_{2} A_{3}$ 共线，一边 $A_{3} A_{6}$ 在 $x$ 轴上 $\dots$ 以此类推，则点 $A_{2022}$ 的坐标为（）

A、 $(672 ， - 1)$ B、 $(673 ， - 1)$ C、 $(674 ， 1)$ D、 $(674 ， 0)$

查看试题解析

二、填空题

7. 比较大小： $\sqrt{10}$ 3．（填“＞”、“=”或“＜”）

查看试题解析
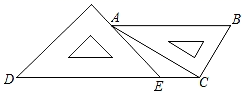
8. 计算： $\sqrt{{(- 5)}^{2}} - \sqrt[3]{27}$ ＝.

查看试题解析
9. 一副三角板按如图所示放置，AB∥DC，则∠CAE的度数为.

查看试题解析
10. 如果M（a，b），N（c，d）是平行于y轴的一条直线上的两点，那么a与c的关系是

查看试题解析
11. 如图是国家级非物质文化遗产——“抖空竹”．在“抖空竹”的一个瞬间如图①所示，若将图①抽象成图②的数学问题： $A B ∥ C D$ ， $∠ E A B = 70 °$ ， $∠ E C D = 110 °$ ，则 $∠ E$ 的大小是度．

查看试题解析
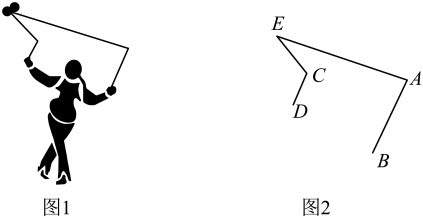12. 小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起，当 $∠ A C E < 180 °$ ，且点E在直线 $A C$ 的上方时，他发现若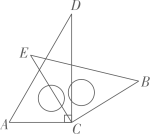 $∠ A C E =$ ，则三角板 $B C E$ 有一条边与斜边 $A D$ 平行.

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt[3]{8} + \sqrt{0} - \sqrt{\frac{1}{4}}$ ；

(2)、 $\frac{1}{2} x^{2} - 2 = 0$ ．

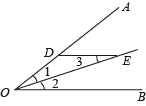
查看试题解析
14. 在平面直角坐标系中，有 $A (- 1 ， 0)$ ，点B在x轴上，且 $A B = 3$ ．

(1)、求点B的坐标；

(2)、若点P在y轴上，且三角形 $A B P$ 的面积为6，求点P的坐标．

查看试题解析
15. 如图，若 $∠ 1 = ∠ 3$ ， DE∥OB，则 $∠ 1$ 与 $∠ 2$ 的关系是，请说明理由．

查看试题解析
16. 小明和他的爸爸、妈妈到运河湿地公园游玩，回到家后，他利用平面直角坐标系画出了公园的景区地图，如图所示，可是他忘记了在图中标出原点、x轴及y轴，只知道长廊E的坐标为 $(4 ， - 3)$ 和农家乐B的坐标为 $(- 5 ， 3)$ ，请你帮他画出平面直角坐标系，并写出其他各点的坐标.

查看试题解析
17. 如图，直线 $A C$ ， $B D$ 相交于点 $O$ ， $O E$ 平分 $∠ A O D$ ，已知： $∠ B O C + 40 ° = ∠ A O B$ ．求 $∠ A O B$ 和 $∠ D O E$ 的度数．

查看试题解析
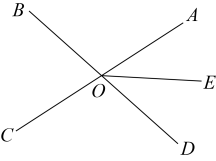18. 如图，已知：点A、B、C在一条直线上．

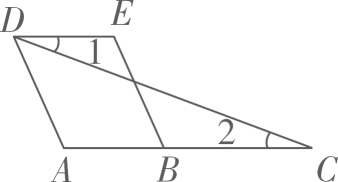(1)、请从三个论断：①AD∥BE； ②∠1=∠2；③∠A=∠E中，选两个作为条件，另一个作为结论构成一个真命题：
条件：

结论：

(2)、证明你所构建的命题是真命题．

查看试题解析
19. 在如图所示的网格纸中，点 $A$ ， $B$ ， $C$ 都在网格点上，请仅用无刻度的直尺按下列要求作图．

(1)、在图 $1$ 中过点 $A$ 画 $B C$ 的垂线 $A P$ ，且点 $P$ 在网格点上．

(2)、在图 $2$ 中画 $∠ B C D = ∠ B$ ，再画 $D E ∥ B C$ ，且点 $D$ ， $E$ 都在网格点上．

查看试题解析
20. 阅读材料：
∵ $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，

∴0＜ $\sqrt{5}$ -2＜1，

∴ $\sqrt{5}$ 的整数部分为2， $\sqrt{5}$ 的小数部分为 $\sqrt{5}$ -2．

解决问题：

(1)、填空： $\sqrt{19}$ 的小数部分是　　；

(2)、已知a是 $\sqrt{90}$ 的整数部分，b是 $\sqrt{3}$ 的小数部分，求a+b- $\sqrt{3}$ 的立方根．

查看试题解析
21. 对于平面直角坐标系 $x O y$ 中的任意一点 $P (x ， y)$ ，给出如下定义：记 $a = - x ， b = x - y$ ，那么我们把点 $M (a ， b)$ 与点 $N (b ， a)$ 称为点P的一对“和美点”．
例如，点 $P (- 1 ， 2)$ 的一对“和美点”是点 $(1 ， - 3)$ 与点 $(- 3 ， 1)$

(1)、点 $A (4 ， 1)$ 的一对“和美点”坐标是与；

(2)、若点 $B (2 ， y)$ 的一对“和美点”重合，则y的值为．

(3)、若点C的一个“和美点”坐标为 $(- 2 ， 7)$ ，求点C的坐标；

查看试题解析
22. 将一副三角板中的两个直角顶点C叠放在一起（如图），其中， $∠ A = 30 °$ ， $∠ B = 60 °$ ， $∠ D = ∠ E = 45 °$ ．

(1)、求证： $∠ A C E + ∠ B C D = 180 °$ ；

(2)、若三角板 $A B C$ 不动，绕顶点C逆时针转动三角板 $D C E$ （不超过一周），当 $C E ∥ A B$ 时，求 $∠ B C D$ 的度数．

查看试题解析
23.
如图，在直角坐标系xOy中，已知A（6，0），B（8，6），将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD．

(1)、写出点C的坐标；

(2)、当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；

(3)、设∠OCD=α，∠DBA=β，∠BDC=θ，判断α、β、θ之间的数量关系，并说明理由．

查看试题解析