山东省济南市槐荫区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 计算:( )A、 B、 C、 D、2. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将0.00000201用科学记数法表示为( )A、 B、 C、 D、3. 下列四个图中, 一定成立的是( )A、
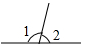 B、
B、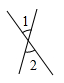 C、
C、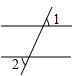 D、
D、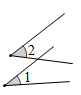 4. 下列命题中,真命题是( )A、在同一平面内,垂直于同一条直线的两条直线互相平行 B、相等的角是对顶角 C、两条直线被第三条直线所截,同位角相等 D、同旁内角互补5. 下列运算中正确的是( )A、 B、 C、 D、6. 用“垂线段最短”来解释的现象是( )A、
4. 下列命题中,真命题是( )A、在同一平面内,垂直于同一条直线的两条直线互相平行 B、相等的角是对顶角 C、两条直线被第三条直线所截,同位角相等 D、同旁内角互补5. 下列运算中正确的是( )A、 B、 C、 D、6. 用“垂线段最短”来解释的现象是( )A、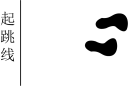 测量跳远成绩
B、
测量跳远成绩
B、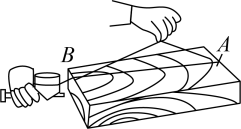 木板上弹墨线
C、
木板上弹墨线
C、 两钉子固定木条
D、
两钉子固定木条
D、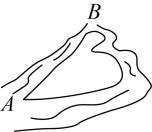 弯曲河道改直
7. 如果是一个完全平方式,则a的值是( )A、3 B、 C、3或 D、9或8. 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
弯曲河道改直
7. 如果是一个完全平方式,则a的值是( )A、3 B、 C、3或 D、9或8. 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( ) A、16° B、33° C、49° D、66°9. 将一副三角尺按不同位置摆放.下列摆放方式中α与β互补的是( )A、
A、16° B、33° C、49° D、66°9. 将一副三角尺按不同位置摆放.下列摆放方式中α与β互补的是( )A、 B、
B、 C、
C、 D、
D、 10. 如果 , 那么代数式的值为( )A、0 B、 C、1 D、3
10. 如果 , 那么代数式的值为( )A、0 B、 C、1 D、3二、填空题
-
11. 计算: .12. 若 , 则的余角为度.13. 计算:14. 如图,C岛在A岛的北偏东方向,C岛在B岛的北偏西方向,则的大小是度.
 15. 如图,已知 , , 以D为圆心,适当长为半径画弧,交于点M,交于点N,再以点N为圆心,长为半径画弧,两弧交于点E.则度.
15. 如图,已知 , , 以D为圆心,适当长为半径画弧,交于点M,交于点N,再以点N为圆心,长为半径画弧,两弧交于点E.则度. 16. 如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
16. 如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
三、解答题
-
17. 计算:18. 计算:;19. 先化简,再求值: , 其中 .20. 如图,已知有四条直线:直线a,直线b,直线m,直线n.若直线 , 直线 .
 (1)、判断直线a与直线b的位置关系,并证明;(推理过程请注明理由)(2)、若 , 求的度数21. 请将解答过程填写完整:
(1)、判断直线a与直线b的位置关系,并证明;(推理过程请注明理由)(2)、若 , 求的度数21. 请将解答过程填写完整:如图, , , 若 , 求的度数.

解:∵(已知)
∴( ).
∵(已知)
∴ ▲ ( ).
∵ ▲ ( ).
∴ ▲ +( ).
∵(已知)
∴ ▲ ( ).
22. 如图,的三个顶点A、B、C在正方形网格中,每个小方格的边长都为1.请在方格纸上画图并回答下列问题: (1)、过C点画直线的垂线,垂足为点E;(2)、过A点画射线 , 交直线于点F;(3)、点C到直线的距离为线段的长度;(4)、比较大小:线段线段(填“>”、“”或“=”).23. 如图,已知 , 被直线所截, .
(1)、过C点画直线的垂线,垂足为点E;(2)、过A点画射线 , 交直线于点F;(3)、点C到直线的距离为线段的长度;(4)、比较大小:线段线段(填“>”、“”或“=”).23. 如图,已知 , 被直线所截, . (1)、试判断B与的位置关系,请说明理由.(2)、若BD平分 , , 求的度数.24.
(1)、试判断B与的位置关系,请说明理由.(2)、若BD平分 , , 求的度数.24.
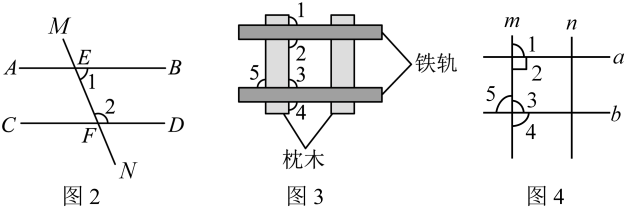 (1)、我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:;(2)、基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”
(1)、我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:;(2)、基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”已知:如图2,∠1和∠2是直线被直线截出的同旁内角,且与互补,求证: . (推理过程请注明理由)
(3)、平行线的判定在实际生活中有许多应用:如图3,在铺设铁轨时,两条铁轨必须是互相平行的.将铁轨和枕木看成直线(如图4 所示,直线a、b为直轨,m、n为枕木),是直角,可以通过度量图中已标出的哪个角的度数,来判断两条铁轨是否平行?为什么?
