山东省烟台市龙口市2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 下列命题是真命题的是( )A、三角形的外角大于它的内角 B、三角形的任意两边之和大于第三边 C、内错角相等 D、直角三角形的两角互余2. 若方程3x2m+1-2yn-1=7是二元一次方程,则m、n的值分别为( )A、m=1,n=1 B、m=l,n=2 C、m=0,n=1 D、m=0,n=23. 用代入法解方程组 时 ,将①代入②得( )A、x-4x+3=6 B、x-4x+6=6 C、x-2x+3=6 D、x-4x-3=64. “掷一枚质地均匀的硬币,正面朝上”这个事件是( )A、不可能事件 B、必然事件 C、随机事件 D、确定事件5. 如图,直线l1∥l2 , 且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为( )
 A、95° B、65° C、85° D、35°6. 如图,在下列给出的条件中,不能判定的是( )
A、95° B、65° C、85° D、35°6. 如图,在下列给出的条件中,不能判定的是( ) A、 B、 C、 D、7. 如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为( )
A、 B、 C、 D、7. 如图,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为( )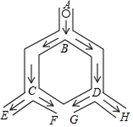 A、 B、 C、 D、8. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、
A、 B、 C、 D、8. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、 B、
B、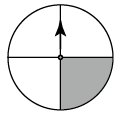 C、
C、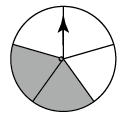 D、
D、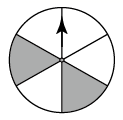 9. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
9. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A、 B、 C、 D、10. 如图所示的几何图形,的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 把命题“直角三角形的两个锐角互余”改写成“如果……那么……”的形式:.12. 把二元一次方程写成用含x的式子表示y的形式为 .13. 如图,某校运会百米预赛用抽签方式确定赛道,若小明第一个抽签,他从1~8号中随机抽取一签,则抽到4号赛道的概率是 .
 14. 如果两数x,y满足 , 那么 .15. 如图,直线和直线相交于点 , 则方程组的解是 .
14. 如果两数x,y满足 , 那么 .15. 如图,直线和直线相交于点 , 则方程组的解是 . 16. 已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球,若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是 , 则y与x之间的函数关系式为 .
16. 已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球,若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是 , 则y与x之间的函数关系式为 .三、解答题
-
17.(1)、用代入消元法解方程组:;(2)、用加减消元法解方程组: .18. 看图填空,在括号内填写理由.
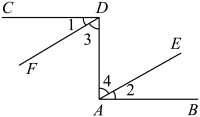
如图,已知 . 试说明 .
证明:(已知),
, ( ),
, ,
又(已知),
( ),
( ).
19. 已知关于x,y的方程组的解也是方程的一组解,求m的值.20. “五·一”期间,某书城为了招徕顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元图书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.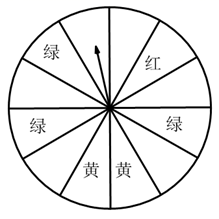 (1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.21. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: .
(1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.21. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: . 22. 甲、乙两地的路程为240千米,一辆汽车从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进到达乙地,设汽车出发x小时后离甲地的路程为y千米,图中折线表示y与x之间的函数关系.
22. 甲、乙两地的路程为240千米,一辆汽车从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进到达乙地,设汽车出发x小时后离甲地的路程为y千米,图中折线表示y与x之间的函数关系. (1)、根据图象可知,汽车行驶的速度为千米/小时;(2)、求线段所表示的y与x之间的函数表达式,并写出x的取值范围.23. 如图,已知 , .
(1)、根据图象可知,汽车行驶的速度为千米/小时;(2)、求线段所表示的y与x之间的函数表达式,并写出x的取值范围.23. 如图,已知 , . (1)、求证:;(2)、 , , 求 .24.
(1)、求证:;(2)、 , , 求 .24. (1)、【问题探究】如图1, , , , 求的度数.(2)、【思维迁移】如图2, , 若点P在B,D两点之间运动,记 , , 问与α,β之间有何数量关系?请写出解题过程.(3)、【拓展延伸】如图3, , 在射线上,若点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),记 , , 请直接写出与α,β之间的数量关系.25. 疫情期间,为满足市场需求,某厂家每天定量生产医用口罩和N95口罩共80万个.当该厂家生产的两种口罩当日全部售出时,则可获得利润35万元.两种口罩的成本和售价如下表所示:
(1)、【问题探究】如图1, , , , 求的度数.(2)、【思维迁移】如图2, , 若点P在B,D两点之间运动,记 , , 问与α,β之间有何数量关系?请写出解题过程.(3)、【拓展延伸】如图3, , 在射线上,若点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),记 , , 请直接写出与α,β之间的数量关系.25. 疫情期间,为满足市场需求,某厂家每天定量生产医用口罩和N95口罩共80万个.当该厂家生产的两种口罩当日全部售出时,则可获得利润35万元.两种口罩的成本和售价如下表所示:成本(元/个)
售价(元/个)
医用口罩
0.8
1.2
N95口罩
2.5
3
(1)、求每天定量生产这两种口罩各多少万个?(列方程组求解)(2)、该厂家将每天生产的口罩打包(每包1万个)并进行整包批发销售.为了支持防疫工作,现从生产的两种口罩中分别抽取若干包口罩免费捐赠给疫情严重的地区,且捐赠的N95口罩包数不超过医用口罩的包数.若该企业把捐赠后剩余的口罩全部售出后,每日仍可盈利2万元,求从医用口罩和N95口罩中各抽取多少包?