山东省济南市市中区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 下列各式运算正确的是( )A、 B、 C、 D、2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有克,用科学记数法表示此数正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
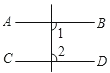 B、
B、 C、
C、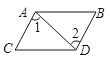 D、
D、 4. 在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度()与下滑的时间()的关系如下表:
4. 在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度()与下滑的时间()的关系如下表:支撑物高()
10
20
30
40
50
…
下滑时间()
3.25
3.01
2.81
2.66
2.56
…
以下结论错误的是( )
A、当时,约2.66秒 B、随支撑物高度增加,下滑时间越来越短 C、支撑物高度每增加了 , 时间就会减少0.24秒 D、估计当时,一定小于2.56秒5. 一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形6. 下列给出的线段长度不能与4 , 3能构成三角形的是( )A、4 B、3 C、2 D、17. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、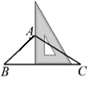 B、
B、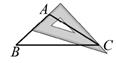 C、
C、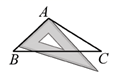 D、
D、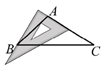 8. 下列命题中,真命题有( )
8. 下列命题中,真命题有( )①在同一平面内,两边分别平行的两角相等;②两条直线被第三条直线所截,内错角相等;③三角形的三条高线所在直线交于一点;④如果 , 那么;⑤过一点有且只有一条直线与已知直线平行
A、1个 B、2个 C、3个 D、4个9. 如图,已知直线l1∥l2 , 直线l与l1 , l2分别相交于点A,B,把一块含30°角的直角三角尺按如图位置摆放,若∠1=130°,则∠ABD的度数为( ) A、15° B、20° C、25° D、30°10. 如图,长为 , 宽为的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的是( )
A、15° B、20° C、25° D、30°10. 如图,长为 , 宽为的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的是( )
①小长方形的较长边为;
②阴影A的较短边和阴影B的较短边之和为;
③若x为定值,则阴影A和阴影B的周长和为定值;
④当时,阴影A和阴影B的面积和为定值.
A、①③ B、②④ C、①③④ D、①④二、填空题
-
11. 若 , , 则 .12. 如果a2+(k-1)ab+9b2是一个完全平方式,那么k= .13. 一个角比它的补角的少40°,这个角等于 .14. 太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点照射到抛物线上的光线 , 等反射以后沿着与平行的方向射出.图中如果 , , 则 , .
 15. 如图甲所示三角形纸片中, , 将纸片沿过点B的直线折叠,使点C落到边上的E点处,折痕为(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为(如图丙),则的大小为°.
15. 如图甲所示三角形纸片中, , 将纸片沿过点B的直线折叠,使点C落到边上的E点处,折痕为(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为(如图丙),则的大小为°. 16. 已知动点P以每秒2cm的速度沿图1的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S(cm2)与时间t(秒)之间的关系如图2中的图象所示.其中AB=6cm,a= , 当t=时,△ABP的面积是18cm2 .
16. 已知动点P以每秒2cm的速度沿图1的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S(cm2)与时间t(秒)之间的关系如图2中的图象所示.其中AB=6cm,a= , 当t=时,△ABP的面积是18cm2 .
三、解答题
-
17. 计算:(1)、;(2)、 .18.(1)、(2)、先化简,再求值: , 其中 , .19. 完成下面的推理过程.
已知:如图,与互补, , 求证: .

证明:∵与互补,即 ▲ ,
∴//( ).
∴( ).
又∵ , (已知).
∴ , 即 . ( ).
∴ ▲ // ▲ ( ).
∴ . ( ).
20. 如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线. (1)、若△ABC的面积为80,BD=10,求AF的长;(2)、若∠BED=40°,∠BAD=25°,求∠BAF的大小.21. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)、若△ABC的面积为80,BD=10,求AF的长;(2)、若∠BED=40°,∠BAD=25°,求∠BAF的大小.21. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题: (1)、图中的自变量是 , 因变量是;(2)、无人机在75米高的上空停留的时间是分钟;(3)、在上升或下降过程中,无人机的速度为米/分;(4)、图中a表示的数是;b表示的数是;(5)、图中点A表示 .22. “五一”假期,小明一家将随团到某风景区旅游,集体门票的收费标准是:25人以内(含25人),每人30元;超过25人时,超过部分每人20元.(1)、写出应收门票费y(元)与游览人数x(人)之间的关系式;(2)、若小明一家所在的旅游团购门票花了1250元,则该旅游团共有多少人.23. 阅读下列材料,完成相应的任务:
(1)、图中的自变量是 , 因变量是;(2)、无人机在75米高的上空停留的时间是分钟;(3)、在上升或下降过程中,无人机的速度为米/分;(4)、图中a表示的数是;b表示的数是;(5)、图中点A表示 .22. “五一”假期,小明一家将随团到某风景区旅游,集体门票的收费标准是:25人以内(含25人),每人30元;超过25人时,超过部分每人20元.(1)、写出应收门票费y(元)与游览人数x(人)之间的关系式;(2)、若小明一家所在的旅游团购门票花了1250元,则该旅游团共有多少人.23. 阅读下列材料,完成相应的任务:三角形数
古希腊著名数学家的毕达哥拉斯学派把1,3,6,10,...,这样的数称为“三角形数”,第n个“三角形数”可表示为: .
发现:每相邻两个“三角形数”的和有一定的规律.如:;;;…
(1)、第5个“三角形数”与第6个“三角形数”的和为;(2)、第n个“三角形数”与第个“三角形数”的和的规律可用下面等式表示:+= , 请补全等式并说明它的正确性 .24. 有两个正方形A,B,边长分别为 , b(a>b).现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙. (1)、用 , b表示图甲阴影部分面积:;用 , b表示图乙阴影部分面积: .(2)、若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .(3)、在(2)的条件下,三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.25. 以直线上一点O为端点作射线 , 使 , 将一个直角角板的直角顶点放在O处,即 .
(1)、用 , b表示图甲阴影部分面积:;用 , b表示图乙阴影部分面积: .(2)、若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .(3)、在(2)的条件下,三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.25. 以直线上一点O为端点作射线 , 使 , 将一个直角角板的直角顶点放在O处,即 . (1)、如图1,若直角三角板的一边放在射线上,则;(2)、如图2,将直角三角板绕点O顺时针转动到某个位置,
(1)、如图1,若直角三角板的一边放在射线上,则;(2)、如图2,将直角三角板绕点O顺时针转动到某个位置,①若恰好平分 , 则;
②若在内部,请直接写出与有怎样的数量关系;
(3)、将直角三角板绕点O顺时针转动(与重合时为停止)的过程中,恰好有 , 求此时的度数.26. 珠江某河段两岸安置了两座可旋转探照灯A,B.如图1,2所示,假如河道两岸是平行的, , 且 , 灯A射线从开始顺时针旋转至便立即回转,灯B射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视,且灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. (1)、填空:°;(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行?(3)、如图3,若两灯同时转动,在灯A射线到达之前,若两灯发出的射线与交于点C,过C作交PQ于点D,且 , 则在转动过程中,请探究与的数量关系,并说明理由.
(1)、填空:°;(2)、若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行?(3)、如图3,若两灯同时转动,在灯A射线到达之前,若两灯发出的射线与交于点C,过C作交PQ于点D,且 , 则在转动过程中,请探究与的数量关系,并说明理由.